
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач 5 страница
Или, вращая буравчик так, чтобы направление его поступательного движения совпадало с направлением тока в проводнике, по направлению вращения ручки буравчика получим направление вектора магнитной индукции (направление вращение ручки буравчика совпадает с направлением вектора магнитной индукции): в левой относительно PP/ части контура вектор магнитной индукции  будет направлен перпендикулярно к этому контуру (или к рамке) вверх (перпендикулярно к чертежу на нас), в правой относительно перемычки PP/ части контура вектор магнитной индукции
будет направлен перпендикулярно к этому контуру (или к рамке) вверх (перпендикулярно к чертежу на нас), в правой относительно перемычки PP/ части контура вектор магнитной индукции  будет направлен перпендикулярно к этому контуру (или к рамке) вниз (перпендикулярно к чертежу от нас).
будет направлен перпендикулярно к этому контуру (или к рамке) вниз (перпендикулярно к чертежу от нас).

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции  имеет одно и то же значение. В противном случае магнитное поле называется неоднородным.
имеет одно и то же значение. В противном случае магнитное поле называется неоднородным.
Потоком вектора  магнитной индукции (магнитным потоком) сквозь малую поверхность площадью dS называется физическая величина
магнитной индукции (магнитным потоком) сквозь малую поверхность площадью dS называется физическая величина
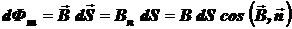 ,
,
где  ‑ вектор площадки,
‑ вектор площадки,
 ‑ единичный вектор нормали к площадке dS,
‑ единичный вектор нормали к площадке dS,
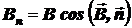 ‑ проекция вектора
‑ проекция вектора  на направление нормали (вектор
на направление нормали (вектор  ).
).
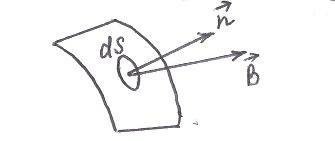
Малая площадка dS выбирается так, чтобы её можно было считать плоской, а значения вектора  всюду в её пределах – одинаковыми.
всюду в её пределах – одинаковыми.
Магнитный поток сквозь произвольную поверхность S:
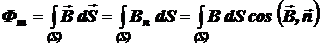 .
.
При вычислении этого интеграла векторы  нормалей к площадкам dS нужно направлять в одну и ту же сторону по отношению к поверхности S. Например, если поверхность S замкнутая, то векторы
нормалей к площадкам dS нужно направлять в одну и ту же сторону по отношению к поверхности S. Например, если поверхность S замкнутая, то векторы  должны быть либо все внешними нормалями, либо все внутренними нормалями. Если магнитное поле однородно, а поверхность S плоская, то
должны быть либо все внешними нормалями, либо все внутренними нормалями. Если магнитное поле однородно, а поверхность S плоская, то
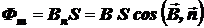 .
.
Электромагнитной индукцией называется возникновение электродвижущей силы в проводнике при его перемещении в магнитном поле либо в замкнутом проводящем контуре вследствие его движения в магнитном поле или изменения самого поля. Эта электродвижущая сила eинд. называется электродвижущей силой электромагнитной индукции. Под её влиянием в замкнутом проводнике возникает электрический ток, называемый индукционным током.
Закон электромагнитной индукции (закон Фарадея ‑ Максвелла): ЭДС eинд. электромагнитной индукции в контуре пропорциональна и противоположна по знаку скорости изменения магнитного потока Фm сквозь поверхность, натянутую на этот контур, т.е.
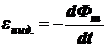 .
.
При этом несущественно, чем именно вызвано изменение магнитного потока – деформацией контура, его перемещением в магнитном поле или изменением самого поля с течением времени. Направление обхода контура при вычислении eинд. и направление нормали  при вычислении Фm должны быть согласованы по правилу правого винта: из конца вектора
при вычислении Фm должны быть согласованы по правилу правого винта: из конца вектора  обход контура должен быть виден происходящим против часовой стрелки.
обход контура должен быть виден происходящим против часовой стрелки.
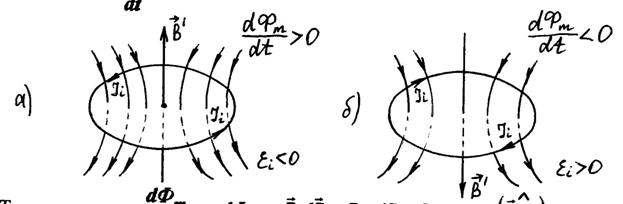
Знак «‑» в правой части закона электромагнитной индукции соответствует правилу Ленца: при всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему индукционный ток.
На нижеприведённом рисунке показаны направления индукционного тока Ii в замкнутом контуре и вектора магнитной индукции 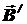 магнитного поля индукционного тока для двух случаев: усиления внешнего магнитного поля (
магнитного поля индукционного тока для двух случаев: усиления внешнего магнитного поля (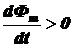 , рис. а) и его ослабления (
, рис. а) и его ослабления ( , рис. б).
, рис. б).
Так как 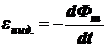 , а
, а 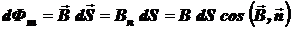 , то
, то
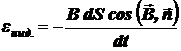 .
.
ЭДС электромагнитной индукции возникает в каждом отрезке проводника, пересекающем при своём движении линии магнитной индукции поля. Перемычка PP/ пересекает при своём движении линии магнитной индукции поля. Значит, в ней возникает ЭДС электромагнитной индукции.
Действительно, при движении перемычки PP/, которая делит рамку на два контура, изменяется площадь поверхности S (каждого контура), пронизываемой потоком вектора  магнитной индукции (магнитным потоком). Значит, изменяется и магнитный поток Фm (
магнитной индукции (магнитным потоком). Значит, изменяется и магнитный поток Фm ( ;
;  ) через оба контура:
) через оба контура:  . Следовательно, в обоих контурах наводится ЭДС индукции:
. Следовательно, в обоих контурах наводится ЭДС индукции: 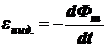 . Так как магнитный поток через правый контур (см. рис.) уменьшается, а через левый увеличивается с одинаковой скоростью, то ЭДС индукции равны по модулю и имеют разные знаки по отношению к заданному направлению обхода контуров:
. Так как магнитный поток через правый контур (см. рис.) уменьшается, а через левый увеличивается с одинаковой скоростью, то ЭДС индукции равны по модулю и имеют разные знаки по отношению к заданному направлению обхода контуров:
 .
.

По условию задачи линии индукции однородного магнитного поля перпендикулярны к плоскости рамки (значит, и вектор  магнитной индукции перпендикулярен к плоскости рамки); вектор
магнитной индукции перпендикулярен к плоскости рамки); вектор  тоже перпендикулярен к плоскости рамки (
тоже перпендикулярен к плоскости рамки ( ‑ вектор нормали к площадке dS). Следовательно,
‑ вектор нормали к площадке dS). Следовательно,
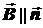 .
.
Векторы  и
и  либо сонаправлены, либо противоположно направлены. Если
либо сонаправлены, либо противоположно направлены. Если  и
и  сонаправлены (
сонаправлены ( ), то
), то 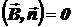 и, следовательно,
и, следовательно, 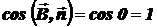 ,
, 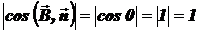 . Если
. Если  и
и  противоположно направлены (
противоположно направлены ( ), то
), то 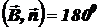 и, следовательно,
и, следовательно, 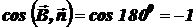 ,
, 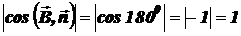 .
.
Видно, что, если 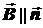 , то неважно, сонаправлены ли векторы
, то неважно, сонаправлены ли векторы  и
и  или противоположно направлены. В любом случае
или противоположно направлены. В любом случае
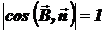 .
.
Значит,
 .
.
Найдём, по какому закону изменяется площадь поверхности S левого контура, пронизываемой потоком вектора  магнитной индукции (магнитным потоком), при движении перемычки PP/ из точки O в центр квадрата E.
магнитной индукции (магнитным потоком), при движении перемычки PP/ из точки O в центр квадрата E.
Если перемычка PP/ находится в точке O, то
S = 0.
Если перемычка пересекает центр квадрата E (центр куска перемычки, по которому (куску перемычки) будет идти ток, также будет находиться в точке E), то
S = SD OAC.
Поскольку OABC – квадрат, то диагонали OB и AC
1) равны:
OB = AC
(обозначим OB = AC = l);
2) пересекаются и точкой пересечения делятся пополам:
 ,
,
 ,
,
где E – точка пересечения диагоналей OB и AC ( );
);
т.е.
 ;
;
3) пересекаются под прямым углом:
OB ^ AC.
Площадь D OAC
 .
.
Таким образом, при движении перемычки из точки O в центр квадрата (точку E) площадь поверхности левого контура, пронизываемой потоком вектора  магнитной индукции (магнитным потоком), изменяется от 0 до
магнитной индукции (магнитным потоком), изменяется от 0 до  .
.
Проведём через точки O и B ось x, начало которой выберем в точке O. Тогда координата точки E:
 .
.
Площадь D OAC перепишем иначе:
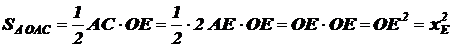 ,
,
здесь использовались равенства: AC = 2 AE, AE = OE, OE = xE.
(Действительно,  (см. выше), а
(см. выше), а  . Значит, SD OAC = xE2.)
. Значит, SD OAC = xE2.)
Таким образом, площадь поверхности S левого контура, пронизываемой потоком вектора  магнитной индукции (магнитным потоком), при движении перемычки PP/ из точки O в центр квадрата E изменяется по следующему закону:
магнитной индукции (магнитным потоком), при движении перемычки PP/ из точки O в центр квадрата E изменяется по следующему закону:
S = x2,
где x – координата центра куска перемычки, по которому (куску перемычки) идёт ток.
В момент, когда перемычка достигает центра квадрата E,  .
.
Следовательно,
 ,
,
где  ‑ проекция на ось x скорости движения перемычки по рамке.
‑ проекция на ось x скорости движения перемычки по рамке.
Но так как
ux = u,
то
 .
.
Обобщённый закон Ома для произвольного участка цепи AC имеет вид:
IRAC = UAC = (jA ‑ jC) + eAC,
где RAC – сопротивление между точками A и C;
UAC ‑ напряжение между точками A и C;
(jA ‑ jC) – разность потенциалов на концах участка AC;
eAC – ЭДС всех источников электрической энергии, включенных на участке цепи AC.
В такой форме закон Ома применим как для пассивных участков цепи, не содержащих источников электрической энергии, так и для активных участков, содержащих такие источники.
В неразветвлённой замкнутой электрической цепи сила тока во всех сечениях одинакова, а сама цепь является участком с совпадающими концами 1 и 2 (см. рис. ниже). В такой цепи j1 = j2 и RAC = R – общее сопротивление всей цепи (в нашем случае, когда мы рассматриваем контур OACO, сопротивление R = ROACO).

Закон Ома для замкнутой электрической цепи:
IR = e,
где e ‑ алгебраическая сумма всех ЭДС, приложенных в цепи.
Так как перемычка и рамка замкнуты, ЭДС в цепи – это ЭДС индукции:
 ;
;
сопротивление рассматриваемого контура OACO есть ROACO:
R = ROACO;
ток, который течёт через перемычку в тот момент, когда она пересекает центр квадрата E (т.е.  ), равен I, то
), равен I, то
 .
.
Найдём сопротивление контура OACO т.е. ROACO:
ROACO = ROA + ROC + RAC.
Сопротивлением R участка цепи между сечениями a и b называется интеграл
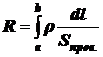 ,
,
где r ‑ удельное электрическое сопротивление среды (в данном случае проволоки, из которой выполнены рамка и перемычка),
dl – длина малого участка проводника (в данном случае проволоки),
Sпров. – площадь поперечного сечения проводника.
Для однородного проводника постоянного сечения (что и представляет собой в данной задаче проволока) r = const, Sпров. = const и
 ,
,
где lab – длина проводника между сечениями a и b.
Длина перемычки PP/, по которой течёт ток I, когда она находится в центре квадрата, равна AC = l. Значит, её сопротивление
 .
.
Если сопротивлением рамки пренебречь, т.е. (рассматривая участок OACO) ROA = ROC = 0, то
 .
.
Тогда при подстановке в уравнение 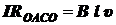 получим
получим
 ,
,
откуда
 .
.
Если сопротивлением рамки не пренебрегать, то с учётом того, что рамка и перемычка выполнены из одного куска проволоки с удельным электрическим сопротивлением r и площадью поперечного сечения Sпров.,
 .
.
Здесь lOA = OA было найдено из теоремы Пифагора: так как рамка квадратная (т.е. OABC ‑ квадрат), то D OAC – прямоугольный (Ð O = 900), значит,
AC2 = OA2 + OC2.
OA = OC как стороны квадрата, AC = l. Следовательно,
 .
.
Таким образом,
 ,
,
 .
.
Зная ROA, ROC и RAC, найдём ROACO:
 .
.
Тогда при подстановке в уравнение 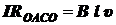 получим
получим
 ,
,
откуда
 .
.

Ответ: если сопротивлением рамки пренебречь, то  ;
;
если сопротивлением рамки не пренебрегать, то  ;
;
в левой относительно PP/ части контура вектор магнитной индукции  направлен перпендикулярно к этому контуру (или к рамке) вверх (перпендикулярно к чертежу на нас);
направлен перпендикулярно к этому контуру (или к рамке) вверх (перпендикулярно к чертежу на нас);
в правой относительно перемычки PP/ части контура вектор магнитной индукции  направлен перпендикулярно к этому контуру (или к рамке) вниз (перпендикулярно к чертежу от нас).
направлен перпендикулярно к этому контуру (или к рамке) вниз (перпендикулярно к чертежу от нас).
25. Определить магнитную индукцию B поля, создаваемого отрезком бесконечно длинного провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии R = 4 см от его середины. Длина отрезка провода l = 20 см, а сила тока в проводе I = 10 А.
| Дано: R = 4 см = 4×10-2 м l = 20 см = 2×10-1 м I = 10 А | Решение. Для магнитного поля, так же как для электрического, справедлив принцип суперпозиции: магнитная индукция поля произвольной системы проводников с токами (или системы отдельных движущихся электрически заряжен- |
| B ‑? |
ных частиц)равна геометрической сумме магнитных индукций полей всех малых элементов этих проводников (соответственно каждой из движущихся заряженных частиц).
Принцип суперпозиции электрических полей (принцип независимости действия электрических полей): напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности.
Магнитная индукция  поля малого элемента проводника длиной dl, по которому течёт постоянный электрический ток силой I, удовлетворяет закону Био – Савара – Лапласа:
поля малого элемента проводника длиной dl, по которому течёт постоянный электрический ток силой I, удовлетворяет закону Био – Савара – Лапласа:
 ,
,
где  ‑ радиус-вектор, проведённый из элемента проводника
‑ радиус-вектор, проведённый из элемента проводника  в рассматриваемую точку поля, т.е. в точку поля, в которой определяется магнитная индукция;
в рассматриваемую точку поля, т.е. в точку поля, в которой определяется магнитная индукция;
m0 = 4p×10-7 Гн/м – магнитная постоянная;
m ‑ магнитная проницаемость среды. В вакууме m = 1.
Из закона Био – Савара – Лапласа следует, что
 ,
,
где j ‑ угол между векторами  и
и  .
.

Из рисунка видно, что
 ,
,
 .
.
Значит,
 .
.
Интегрируя левую и правую части уравнения, получим
 .
.
Рассмотрим отдельно правую часть:
 ,
,
где обозначили  .
.
Таким образом,
 ,
,
где константу интегрирования C можно найти из граничных условий:
при l ® ¥ (т.е. для прямого бесконечно длинного проводника, а по условию задачи данный проводник бесконечно длинный) индукция магнитного поля 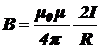 (R – кратчайшее расстояние от проводника до точки, в которой подсчитывается индукция поля).
(R – кратчайшее расстояние от проводника до точки, в которой подсчитывается индукция поля).
Значит (при подстановке в  длины l ® ¥ должно получиться
длины l ® ¥ должно получиться 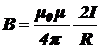 ),
),
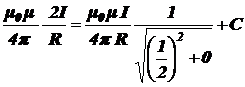 ,
,
откуда
 .
.
Следовательно, магнитная индукция B поля, создаваемого отрезком бесконечно длинного провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии R от его середины, равна
 .
.
 .
.
Ответ:  .
.
26. Круговой виток радиусом R = 15 см расположен относительно бесконечно длинного провода так, что его плоскость параллельна проводу. Перпендикуляр, восстановленный на провод из центра витка, является нормалью к плоскости витка. Сила тока в проводе I1 = 1 А, сила тока в витке I2 = 5 А. Расстояние от центра витка до провода d = 20 см. Определить магнитную индукцию в центре витка.
| Дано: R = 15 см = 15×10-2 м I1 = 1 А I2 = 5 А d = 20 см = 2×10-1 м | Решение. Для магнитного поля, так же как для электрического, справедлив принцип суперпозиции: магнитная индукция поля произвольной системы проводников с токами (или системы отдельных движущихся электрически заряженных частиц) равна геометрической сумме |
| B ‑? |
магнитных индукций полей всех малых элементов этих проводников (соответственно каждой из движущихся заряженных частиц).
Принцип суперпозиции электрических полей (принцип независимости действия электрических полей): напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности.
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током, по которому течёт постоянный электрический ток силой I1, равна
 ,
,
где m0 = 4p×10-7 Гн/м – магнитная постоянная;
m ‑ относительная магнитная проницаемость вещества (среды). В вакууме m = 1;
d – расстояние от провода до рассматриваемой точки поля, в которой необходимо определить магнитную индукцию поля (т.е. расстояние от провода до центра витка);
Магнитная индукция в центре кругового проводника с током
 ,
,
где R – радиус кривизны проводника (витка).
Так как  , где
, где  ‑ вектор бесконечно длинного прямого проводника с током;
‑ вектор бесконечно длинного прямого проводника с током; 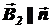 , где
, где  ‑ нормаль к плоскости витка (т.е.
‑ нормаль к плоскости витка (т.е.  перпендикулярен плоскости витка). А так как по условию задачи перпендикуляр, восстановленный на провод из центра витка, является нормалью к плоскости витка, т.е.
перпендикулярен плоскости витка). А так как по условию задачи перпендикуляр, восстановленный на провод из центра витка, является нормалью к плоскости витка, т.е.  , то
, то
 .
.

Не нашли, что искали? Воспользуйтесь поиском: