
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Работа №8. Магнитное поле соленоида
Цель работы: Изучение явления электромагнитной индукции; определение величины поля соленоида.
Краткая теория
Электромагнитной индукцией называют явление возникновения тока в контуре при изменении магнитного потока, пронизывающего этот контур. Открытие электромагнитной индукции Фарадеем в 1831 году было одним из наиболее фундаментальных открытий в электродинамике. Напомним, что магнитным потоком вектора индукции однородного магнитного поля  через плоскую поверхность площади
через плоскую поверхность площади  называют скалярную физическую величину Ф, равную
называют скалярную физическую величину Ф, равную
Ф=ВS соs α (1)
 |
где α — угол, образуемый вектором
 с единичным вектором нормали
с единичным вектором нормали  , проведённым к поверхности
, проведённым к поверхности  (рис. 1).
(рис. 1).
Рис. 1
Выражение для магнитного потока может быть записано в виде
Ф = 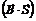 = BnS
= BnS
где Вn= B cos α — проекция вектора  на направление нормали
на направление нормали  . В случае неоднородного магнитного поля
. В случае неоднородного магнитного поля  и поверхности произвольной формы, площадку S можно выбрать настолько маленькой, что в ее пределах магнитное поле меняться не будет. Тогда вычисление магнитного потока Ф сводится к вычислению поверхностного интеграла
и поверхности произвольной формы, площадку S можно выбрать настолько маленькой, что в ее пределах магнитное поле меняться не будет. Тогда вычисление магнитного потока Ф сводится к вычислению поверхностного интеграла
Ф=  =
= 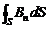 (2)
(2)
Из соотношения (1) видно, что изменить магнитный поток через поверхность, ограниченную некоторым контуром, можно различными способами, например:
а) меняя магнитное поле;
б) меняя площадь о контура;
в) поворачивая контур, меняя угол α и т.п.
Фарадеем было экспериментально установлено, что независимо от способа изменения магнитного потока в конуре возникает электродвижущая сила индукции Eи нд , равная скорости изменения магнитного потока, взятой с обратным знаком:
E инд =  (3)
(3)
где за положительное направление E инд (а, точнее, индукционного тока) принимается направление обхода контура, образующее правовинтовую систему с направлением вектора нормали  (на рисунке 1 это направление показано пунктиром). Уравнение (3) получило название з акона Фарадея для электромагнитной индукции.
(на рисунке 1 это направление показано пунктиром). Уравнение (3) получило название з акона Фарадея для электромагнитной индукции.
Сила индукционного тока Iинд может быть найдена согласно закону Ома для замкнутой цепи:
Iинд= E инд/R (4)
где R — сопротивление (омическое) контура.
Закон Фарадея (3) (совместно с законом Ома (4)) позволяет определить не только величину, но и направление индукционного тока. Действительно, рассмотрим проволочный виток в магнитном поле (риc. 2)

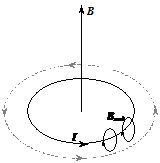
а) б)
Рис. 2
Допустим, что магнитный поток возрастает (dФ/dt >0). Тогда, согласно формуле (3), величина E инд будет отрицательна, а потому индукционный ток потечёт в витке в отрицательном направлении, т.е. так как показано на рис. 2а. Такой ток своим магнитным полем Винд будет препятствовать возрастанию магнитного потока. Пусть теперь магнитный поток убывает (dФ/dt <0). Тогда величина E инд станет положительной, а индукционный ток в витке потечёт в положительном направлении (рис. 2б) и своим магнитным полем будет препятствовать убыванию магнитного потока. Таким образом, индукционный ток всегда имеет такое направление, что своим магнитным полем препятствует изменению магнитного потока, которым он вызван. Это правило впервые было сформулировано Ленцем и носит его имя.
Как известно, электрическим током называют направленное движение заряженных частиц. Какая же сила приводит свободные заряды проводящего контура в направленное движение при изменении магнитного потока? В технических случаях, когда изменение магнитного потока, пронизывающего замкнутый контур, связано с движением частей контура, то возникновение индукционного тока объясняется действием сил Лоренца на свободные заряды подвижных частей. Долгое время было не ясно, какая же сила приводит в движение свободные заряды неподвижного контура, помещённого в переменное магнитное поле? Ответ был дан Максвеллом. Согласно Максвеллу, всякое переменное магнитное поле порождает в окружающем пространстве электрическое поле. Последнее и является причиной возникновения индукционного тока в проводнике. Это электрическое поле имеет замкнутые силовые линии и называется вихревым электрическим полем (в отличие от электростатического поля, силовые линии которого начинаются на положительных зарядах и кончаются на отрицательных). Максвеллу принадлежит следующая углублённая формулировка закона электромагнитной индукции. Всякое изменение магнитного поля во времени порождает в окружающем пространстве электрическое поле. Циркуляция вектора напряжённости  этого поля по любому неподвижному замкнутому контуру Ω определяется выражением
этого поля по любому неподвижному замкнутому контуру Ω определяется выражением
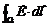 = -
= -  (5)
(5)
где Ф - магнитный поток, пронизывающий контур Ω. Мы использовали для обозначения скорости магнитного потока знак частной, а не полной производной. Этим мы хотим подчеркнуть, что контур Ω должен быть неподвижным. Причем можно показать, что в каждой точке пространства, в любой момент времени 
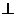
 .
.
Между максвелловским и фарадеевским пониманиями явления электромагнитной индукции имеется существенное различие. Согласно Фарадею, электромагнитная индукция состоит в возбуждении электрического тока. Максвелл, напротив, видит сущность электромагнитной индукции прежде всего в возбуждении электрического поля, ане тока. Электромагнитная индукция может наблюдаться и тогда, когда в пространстве нет никаких проводников. Появление индукционного тока в замкнутом проводнике при внесении последнего в переменное магнитное поле есть лишь одно из проявлений вихревого электрического поля  . Но поле
. Но поле  может производить и другие действия, например, поляризовать диэлектрик, вызвать пробой конденсатора, ускорять и тормозить заряженные частицы и т.п. Максвелловская формулировка закона индукции более общая, чем формулировка Фарадея. Она принадлежит к числу наиболее важных обобщений электродинамики. Математический закон индукции в понимании Максвелла выражается формулой (5), где Ω - произвольный математический замкнутый контур, который может быть проведён и в диэлектрике, а необязательно в проводнике, как было у Фарадея. Принимая во внимание выражение (2) для магнитного потока через поверхность S, ограниченную контуром Ω, формулу (5) можно представить в виде
может производить и другие действия, например, поляризовать диэлектрик, вызвать пробой конденсатора, ускорять и тормозить заряженные частицы и т.п. Максвелловская формулировка закона индукции более общая, чем формулировка Фарадея. Она принадлежит к числу наиболее важных обобщений электродинамики. Математический закон индукции в понимании Максвелла выражается формулой (5), где Ω - произвольный математический замкнутый контур, который может быть проведён и в диэлектрике, а необязательно в проводнике, как было у Фарадея. Принимая во внимание выражение (2) для магнитного потока через поверхность S, ограниченную контуром Ω, формулу (5) можно представить в виде
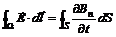

В настоящей лабораторной работе Вам предстоит экспериментально проверить, выполнение соотношений, вытекающих из закона электромагнитной индукции для конкретного случая, о котором речь пойдёт ниже.
Соленоид
Как известно, соленоид представляет собой цилиндрического вида катушку, на которую плотно намотаны витки проволоки. Соленоид, длина которого много больше поперечного диаметра называется длинным. Если по проводу, намотанному на соленоид пропустить электрический ток, то этот ток создаст вокруг себя магнитное поле. С известным приближением, магнитное поле внутри соленоида можно считать однородным, поле же вне соленоида можно считать равным нулю. Индукция магнитного поля внутри соленоида направлена вдоль его оси, а по величине равна:
В = μ0nI = 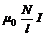 (6)
(6)
где
μ0 - магнитная постоянная,
п – число витков проволоки на единицу длины катушки,
I – сила тока в обмотке катушки,
N – полное число витков катушки,
l – ее длина.
Это однородное магнитное поле внутри соленоида создает магнитный поток через один виток проволоки, равный:
Ф1 = BS
где S – площадь поперечного сечения соленоида, а поток, пронизывающий всю катушку, равен:
Ф = N Ф1 = NBS (7)
Соленоид характеризуется так же индуктивностью L:
 (8)
(8)
Если по проводу, навитому на катушку, течет постоянный электрический ток, то и магнитный поток через соленоид постоянен, т.е.
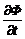 = 0,
= 0,
а это значит, в соответствии с законом электромагнитной индукции, о котором шла речь выше (5), что и
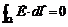
Вообще говоря, отсюда вовсе не следует, что и Е = 0, однако для соленоида это именно так. Действительно, поскольку магнитное поле внутри соленоида однородно, и кроме того как уже отмечалось 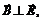 то в силу цилиндрической симметрии силовые линии вихревого электрического поля представляют собой концентрические окружности с центром на оси соленоида. Это показано на рис. 3.
то в силу цилиндрической симметрии силовые линии вихревого электрического поля представляют собой концентрические окружности с центром на оси соленоида. Это показано на рис. 3.
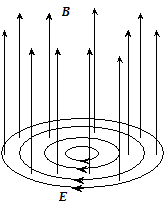
Рис. 3
Значит, выбрав в качестве контура Ω в формуле (5) одну из таких окружностей, (на которой очевидно Е = const) мы можем вынести Е за знак интеграла, получив при этом:
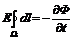
Здесь мы избавились и от скалярного произведения, учитывая, что для выбранного таким образом контура Ω: 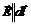 . Тогда из
. Тогда из
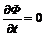
следует очевидно что и Е = 0.
Пусть теперь по проводу, навитому на катушку, течет переменный электрический ток. Тогда в соответствии с (6), магнитная индукция В будет зависеть от времени, оставаясь при этом однородной, а значит и магнитный поток Ф тоже зависит от времени, и
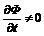
Стало быть, в этом случае существует вихревое электрическое поле, как внутри, так и вне соленоида. Если рассмотреть переменный синусоидальный ток, круговой частоты ω
I(t) = I0 cos ω t
то, как легко убедиться, зависимость напряженности вихревого электрического поля от расстояния r до оси соленоида и от времени t, описывается выражениями:
для поля внутри соленоида:
E(r,t) = 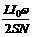 r sin ωt (9)
r sin ωt (9)
и для поля вне соленоида:
E(r,t) =  sin ωt (10)
sin ωt (10)
С соответствующими электродвижущими силами индукции вдоль контура Ω:
внутри соленоида:
E инд= 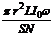 sin ωt
sin ωt
вне соленоида:
E инд = LI0 ω sin ωt
Амплитудное значение индукции магнитного поля внутри соленоида тогда будет
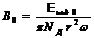 (11)
(11)
где E инд 0 – амплитудное значение Э.Д.С. индукции на расстоянии r от оси соленоида, N Д – число витков датчика.
Но пока это только слова и формулы. Физика же наука экспериментальная. Как же нам проверить истинность предыдущих рассуждений? Если такое вихревое электрическое поле существует, то оно должно в чем-то проявиться. В частности оно должно проявиться в создании электродвижущей силы в проводнике, помещенном в это поле. Таким образом, если мы возьмем замкнутый проводник с известным электрическим сопротивлением, по форме совпадающий с силовой линией вихревого электрического поля, то в нем должен появиться переменный электрический ток, амплитуду (или действующее значение) которого можно измерить.
Описание установки
Схема установки изображена на Рис. 4. Соленоид L представляет собой катушку индуктивности диаметром 76 мм и длиной 750 мм. Плотность его намотки — 1000 витков/метр.
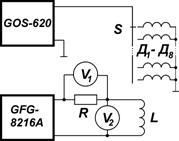
Рис. 4
Генератор подключен к соленоиду L через резистор R, величина которого 1 Ом. При этом показания вольтметра V1 в вольтах будут численно равны величине силы тока в амперах. Вольтметр V2 измеряет напряжение на соленоиде.
Переключатель S позволяет подключить к осциллографу один из восьми датчиков, представляющих собой катушки индуктивности. Датчики Д1 - Д4 расположены внутри соленоида, имеют по 20 витков тонкого провода. Диаметры катушек — 30, 40, 50 и 60 мм. Датчики Д5 - Д8 расположены снаружи соленоида имеют 10 витков и диаметры 110, 140, 170 и 200 мм.
Не нашли, что искали? Воспользуйтесь поиском: