Периодический режим (затухание мало)

Режим малого затухания характеризуется неравенством 0 £ b £ w ₀.

Корни характеристического уравнения (y ² + 2 b y + w ₀² = 0) в этом случае являются комплексно-сопряженными:

y _1,2 = - b ± iw, где 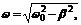i – мнимая единица.

Общее решение уравнения (1) при φ (t) º 0 (без правой части) записывают в виде:

x ₀(t) = A ₀ e ^{- b t} sin(w t+ψ ₀) (2)

где А ₀ и ψ ₀ - произвольные постоянные, определяемые из начальных условий.

Величина А (t) = A ₀ e ^{- b t} называется амплитудой,

φ (t) = w t+ψ ₀ фазой колебания.

Видно, что x ₀(t) в виде (2) содержит периодический множитель, а также убывающую со временем амплитуду. График функции (2) представлен на рис. 2.

Добротностью Q колебательной системы называется отношение максимальных значений силы упругости (kA) к силе трения (w rA). При очень малом затухании (w → w ₀) и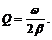

Величина называется логарифмическим декрементом,

где А (t) и А (t+T) – значения амплитуд для моментов времени, различающихся на один период Т.

Легко видеть, что (3)

Критический (переходный) режим (b =w ₀)

Корень характеристического уравнения действительный, отрицательный, двукратный:

y _1,2 = - β

Общее решение, соответствующее критическому режиму, имеет вид:

x ₀(t) = (A ₁ + A ₂ t) e ^{- βt}, (4)

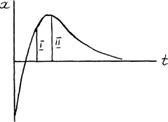
Функция (4) не обладает периодичностью. Общий вид графика функции (4) изображен на рис.3. В зависимости от начальных условий можно наблюдать как всю кривую, так и только ее участки, лежащие справа от вертикалей I или II.

Не нашли, что искали? Воспользуйтесь поиском: