Дифференциальное уравнение вынужденных колебаний

Будем параллельно рассматривать две модели колебательных систем (механическую и электрическую), изображенные на рис.1.

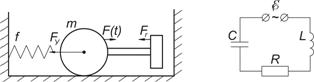
Рис. 1

Каждая из них содержит 4 основных элемента.

1. Квазиупругий, т.е. такой, который стремится уничтожить возникшее возмущение.

1а. Пружина жесткости k, стремящаяся под действием силы упругости (F_У = -kХ) перейти в недеформированное состояние,

1б. Конденсатор (U_C = q/С), стремящийся разрядиться.

2. Инерционный, стремящийся поддерживать движение неизменным.

2a. Масса груза m, (сила инерции F_i = - ma = - m ).

2б. Индуктивность L (э.д.с. самоиндукции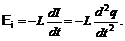

3. Демпфирующий, наличие которого вызывает необратимые потери энергии колебательной системы:

3а. Демпфер, сила сопротивления F_r, которого направлена против вектора скорости и пропорциональна его модулю (F_r = -rv = -rx, закон Стокса);

3б. Омическое сопротивление витков катушки и соединительных проводов (U_R = IR = Rq')

4. Возмущающий элемент, создающий периодическое возбуждение системы;

4а. Сила F(t), приложенная к колеблющемуся телу,

4б. Переменная э.д.с. E (t), включенная в колебательный контур.

Состояние системы (а) описывается 2-м законом Ньютона:

, или mx'' = –kx – rx' + F(t),

системы (б) - 2-ым правилом Кирхгофа (для замкнутых контуров):

Σ U_k = Σ E _k, или

Оба уравнения могут быть представлены в совершенно одинаковом виде:

x'' + 2b x' + w₀²x = φ (t), (1)

где x колеблющаяся величина [а) -смещение точки от положения устойчивого равновесия; б)- мгновенное значение величины заряда q на обкладках конденсатора],

b - коэффициент затухания [а) б)

ω ₀ - циклическая частота свободных колебаний системы при отсутствии потерь энергии

[а) б)

φ (t) - функция, описывающая воздействие возмущающего элемента на колебательную систему

а) 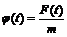б)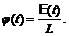

Таким образом, с математической точки зрения обе рассматриваемые колебательные системы эквивалентны друг другу, поскольку протекающие в них процессы описываются единым уравнением (1). * Это линейное неоднородное обыкновенное дифференциальное уравнение 2-го порядка с постоянными коэффициентами для определения неизвестной функции х (t).

Согласно теории линейных неоднородных уравнений, общее решение уравнения (1) является суммой общего решения соответствующего однородного уравнения х ₀ (отличающегося от (1) лишь тем, что φ (t) полагается равной нулю) и любого частного решения х_n (t) уравнения с правой частью (1).

Ясно, что х ₀(t) будет характеризовать свободные колебания (действие возмущающего фактора игнорируется), тогда как х_n (t) характеризует вынужденное движение.

Не нашли, что искали? Воспользуйтесь поиском: