Вынужденные колебания. Резонанс

Как уже говорилось, применительно к колебательным системам интересен только такой случай, когда действие вынуждающего фактора φ (t) является периодическим с периодом Т, то есть φ (t) = φ (t + nT), где n - любое целое число. Поскольку всякая периодическая функция может быть представлена тригонометрическим рядом (рядом Фурье), ясно, что без ущерба общности можно ограничиться исследованием колебаний, возникающих при φ (t) = A ₀ sin (Ω t + Φ), где Ω = 2 π / T. То есть рассматриваемое дифференциальное уравнение (1) вынужденных колебаний фактически имеет вид:

x'' + 2b x' + w₀²x = A ₀ sin (Ω t + Φ). (6)

Частное решение уравнения (6) ищут в виде гармонического колебания, имеющего частоту вынуждающей силы и отстающего по фазе от нее на Ф, что без ущерба общности возможно сделать разумным выбором момента времени t = 0.

Итак:

(7)

Подставляя (7) в (6), раскрывая правую часть (6) по формуле синуса суммы двух углов и группируя коэффициенты при синусах и косинусах, получим:

a ₀cosΦ = A (ω ₀² – Ω²),

a ₀sinΦ = 2 Aβ Ω.

Решая последнюю систему уравнений относительно А и Φ, имеем:

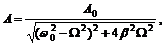(8)

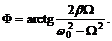(9)

Из формулы (9) видно, что сдвиг фаз Φ между вынуждающей силой и вызываемым ею движением определяется, в основном, коэффициентом затухания β. В частности, если затухание достаточно мало, колебания происходят практически синфазно с вынуждающей силой.

В знаменателе формулы (8) вынесем из под корня ω ₀², тогда

где x ₀ = A ₀/ ω ₀²:

a) - равно статическому смещению груза под действием постоянной силы, равной амплитудному значению F (t),

б) - статическому заряду конденсатора, который сообщит ему постоянная э.д.с., равная амплитудному значению E(t).

Теперь введем представление о коэффициенте динамичности колебательной системы μ, как отношения "динамической" амплитуды к статическому возмущению x ₀. Тогда

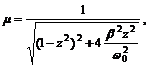(10)

где z = Ω/ ω ₀. (11)

Зависимость μ (z) изображается резонансной кривой. Проанализируем ее вид при различных коэффициентах затухания β.

1) независимо от β, μ (0) = 1.

2) при достаточно малом затухании (b «w ₀, 0 < z £ 1)

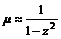- монотонно возрастает от 1.

При z = 1 и b = 0, теоретически μ (z) = ∞.

При z > 1 имеет место монотонный спад μ до 0.

Явление резкого возрастания коэффициента динамичности при приближении z к 1 (то есть при Ω → ω ₀) носит название резонанса.

3) с увеличением b, μ (1) < ∞, полуширина резонансной кривой увеличивается, резонанс становится менее "острым". Положение максимума μ (z) смещается влево.

4) при очень большом затухании b ²/ ω ₀²» 1, выражением (1 – z ²)² под корнем в интервале 0 < z < 2 можно пренебречь по сравнению со вторым слагаемым, поэтому 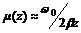ведет себя подобно гиперболе z ^. μ = const. Система резонансных кривых при различных коэффициентах затухания b представлена на рис.4, где с увеличением порядкового номера кривой коэффициент затухания возрастает.

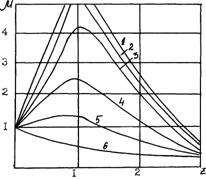
Рис.4

Описание установки

Принципиальная схема установки изображена на рис.5.

Рис.5

Генератор подзаряжает конденсатор. Переменное напряжение на обкладках конденсатора подается на вход Y осциллографа. Разряд конденсатора происходит в практически изолированном колебательном LRC - контуре (поскольку выход генератора имеет малое сопротивление, а вход осциллографа очень большое).

В качестве катушки используется соленоид L, конденсатор C имеет емкость 10 нФ.

Не нашли, что искали? Воспользуйтесь поиском: