Сложение гармонических колебаний одного направления с одинаковыми частотами

Гармоническим колебанием называется простое периодическое колебание, при котором смещение X меняется со временем по закону косинуса или синуса.

X₁=A₁× cos(w t + j₁),

X₂=A₂× cos(w t + j₂)

X=A× cos(w t + j),

в котором частота w остается прежней, а амплитуда A и начальная фаза j окажутся равными:

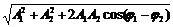tgj=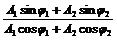

Аналогичный случай сложения справедлив также для электрических колебаний, в которых роль смещения X и его амплитудных значений A выполняют: заряд q, сила тока I или напряжение U.

Сложение колебаний можно наглядно представить в виде векторной диаграммы (рис.1).

На этой диаграмме: A₁ и A₂ – амплитуды, X₁ и X₂ – смещения, j₁ и j₂ начальные фазы складывающихся колебаний; A, X и j – соответственно амплитуда, смещение и начальная фаза результирующего колебания. Если привести вектора во вращение с угловой скоростью w, то их проекции будут перемещаться по оси X в пределах амплитудных значений от –A до +A, причем координаты этих проекций будут изменяться по закону: X=A× cos(w t+j). Следовательно, проекции векторов на оси X будут совершать гармонические колебания с амплитудами, равными длине векторов, угловыми частотами, равными угловой скорости вращения векторов, и начальными фазами, равными углам, образуемым векторами с осью в начальный момент времени.

Не нашли, что искали? Воспользуйтесь поиском: