
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Одно из уравнений Максвелла представляет собой обобщение закона полного тока для поля в веществе и математически может быть выражено уравнениями
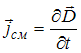

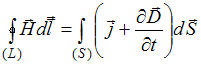
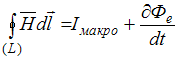
Решение
Максвелл обобщил закон полного тока, предположив, что переменное электрическое поле наряду с токами проводимости является источником магнитного поля:
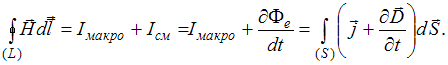
Задание №16
Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3, причем поверхность S3 охватывает поверхность S2, которая в свою очередь охватывает поверхность S1 (рис.).
 Поток напряженности электростатического поля отличен от нуля сквозь...
Поток напряженности электростатического поля отличен от нуля сквозь...
поверхности S2 и S3 поверхность S2
поверхность S3 поверхность S1
Решение
Согласно теореме Остроградского – Гаусса, поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы электрических зарядов, охватываемых этой поверхностью, и электрической постоянной  , т.е.
, т.е.  . Из условия видим, что
. Из условия видим, что 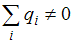 только для поверхности S1, поэтому поток напряженности электростатического поля отличен от нуля сквозь поверхность S1.
только для поверхности S1, поэтому поток напряженности электростатического поля отличен от нуля сквозь поверхность S1.
Задание №17
На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с одинаково направленными токами, причем 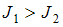 . Индукция
. Индукция 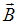 результирующего магнитного поля равна нулю в некоторой точке интервала …
результирующего магнитного поля равна нулю в некоторой точке интервала …
 c b d a
c b d a
Решение
Линии магнитной индукции прямолинейных длинных проводников с токами 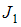 и
и  представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта соответствует направлению тока в проводнике. Направления векторов магнитной индукции
представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта соответствует направлению тока в проводнике. Направления векторов магнитной индукции 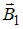 и
и  в некоторых точках интервалов
в некоторых точках интервалов  совпадают с касательными к линиям магнитной индукции в этих точках поля и показаны на рисунке.
совпадают с касательными к линиям магнитной индукции в этих точках поля и показаны на рисунке.

Индукция 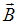 результирующего магнитного поля определяется по принципу суперпозиции
результирующего магнитного поля определяется по принципу суперпозиции 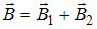 и равна нулю, если векторы
и равна нулю, если векторы 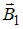 и
и  противоположно направлены и равны по модулю. Это может быть только в точках интервалов
противоположно направлены и равны по модулю. Это может быть только в точках интервалов  и
и 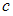 . Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле
. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле  , то модули векторов
, то модули векторов 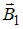 и
и  равны, если
равны, если  , т.к. по условию
, т.к. по условию  . Следовательно, индукция
. Следовательно, индукция 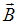 результирующего магнитного поля равна нулю в некоторой точке интервала c.
результирующего магнитного поля равна нулю в некоторой точке интервала c.
Задание №18
Вещество является однородным изотропным парамагнетиком, если магнитная восприимчивость …
мала, вектор намагниченности направлен в сторону, противоположную направлению вектора напряженности внешнего магнитного поля
много больше единицы ( ), вектор намагниченности направлен в ту же сторону, что и вектор напряженности внешнего магнитного поля
), вектор намагниченности направлен в ту же сторону, что и вектор напряженности внешнего магнитного поля
мала, вектор намагниченности направлен в ту же сторону, что и вектор напряженности внешнего магнитного поля
много больше единицы ( ), вектор намагниченности направлен в сторону, противоположную направлению вектора напряженности магнитного поля
), вектор намагниченности направлен в сторону, противоположную направлению вектора напряженности магнитного поля
Решение
К парамагнетикам относятся вещества, атомы (молекулы) которых обладают собственным магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно в отсутствие внешнего магнитного поля, и намагниченность вещества в этих условиях равна нулю. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов (молекул) в направлении поля. Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным. Магнитная восприимчивость парамагнетиков положительна, значительно меньше единицы и составляет величину 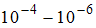 .
.
Задание№19
В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией  . Вектор напряженности электрическогополя в точке А будет иметь направление, показанноещстрелкой …
. Вектор напряженности электрическогополя в точке А будет иметь направление, показанноещстрелкой …
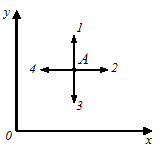
2 3 4 1
Решение
Связь напряженности и потенциала электростатического поля имеет вид:  , или в проекциях на оси прямоугольной декартовой системы координат:
, или в проекциях на оси прямоугольной декартовой системы координат:  ,
,  ,
, 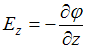 . Так как по условию потенциал
. Так как по условию потенциал 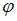 зависит только от y, отлична от нуля только
зависит только от y, отлична от нуля только  и
и 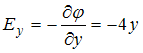 . Таким образом, вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой 3.
. Таким образом, вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой 3.
Задание №20
Установите соответствие между уравнениями Максвелла и их физическим смыслом.
1.  2.
2.  3.
3. 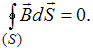
Изменяющееся со временем магнитное поле порождает вихревое электрическое поле
Источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле.
«Магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
Источником электрического поля являются свободные электрические заряды
Решение
Уравнение 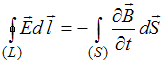 означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле. Из уравнения
означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле. Из уравнения  следует, что переменное электрическое поле наряду с токами проводимости является источником вихревого магнитного поля. Уравнение
следует, что переменное электрическое поле наряду с токами проводимости является источником вихревого магнитного поля. Уравнение 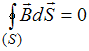 означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.
означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.
Задание №21
На рисунке показана зависимость силы тока i, протекающего в катушке индуктивности, от времени t.

Изменение возникающей в катушке ЭДС самоиндукции  от времени правильно изображено на рисунке …
от времени правильно изображено на рисунке …
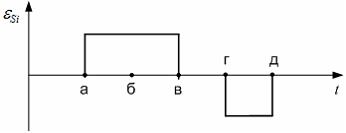
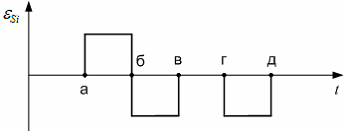

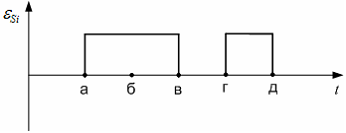 Решение
Решение
ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока i в контуре: 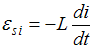 , где L – индуктивность контура. Следовательно:
, где L – индуктивность контура. Следовательно:
1) если сила тока не изменяется со временем, т.е. i = const, то  ;
;
2)если сила тока возрастает, т.е.  >0, то
>0, то  <0;
<0;
3)если сила тока убывает, т.е.  <0, то
<0, то  >0;
>0;
4) если сила тока I изменяется со временем по линейному закону, т.е.  , то
, то  = const, т.к. в этом случае
= const, т.к. в этом случае  = const.
= const.
Поэтому зависимость возникающей в катушке ЭДС самоиндукции  от времени правильно изображено на рисунке
от времени правильно изображено на рисунке
 Задание №22
Задание №22
Для электронной поляризации диэлектриков характерно …
влияние теплового движения молекул на степень поляризации диэлектрика
ориентирующее действие внешнего электрического поля на собственные дипольные моменты молекул
возникновение у молекул индуцированного дипольного момента при помещении диэлектрика во внешнее электрическое поле
смещение подрешетки положительных ионов по направлению вектора напряженности внешнего электрического поля, а отрицательных – против поля
Решение
Молекулы некоторых диэлектриков имеют симметричное строение, то есть центры распределения положительных и отрицательных зарядов в молекуле в отсутствие внешнего электрического поля совпадают, и дипольный момент молекулы равен нулю. Поэтому молекулы таких диэлектриков называются неполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля), и молекула приобретает дипольный момент. Внесение диэлектрика в электрическое поле приводит к его поляризации. Такой тип поляризации называется электронной. Следовательно, электронная или деформационная поляризация диэлектрика с неполярными молекулами заключается в возникновении у молекул индуцированного дипольного момента за счет деформации электронных орбит под влиянием внешнего электрического поля. Тепловое движение неполярных молекул никак не влияет на возникновение у них индуцированных электрических моментов, которые всегда совпадают по направлению с вектором напряженности электрического поля (это связано с очень малой инертностью электронов).
Задание№23
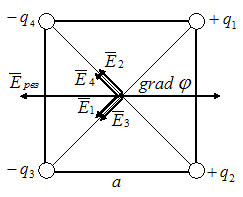
Каждый из четырех одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создает в точке пересечения диагоналей электрическое поле, напряженность которого равна  .
.

Градиент потенциала поля в этой точке равен _______и направлен горизонтально …
 , влево
, влево  , влево
, влево
 , вправо
, вправо  , вправо
, вправо
Решение
Градиент потенциала в некоторой точке связан с напряженностью поля в этой точке соотношением:  . Поэтому для нахождения
. Поэтому для нахождения  в точке пересечения диагоналей квадрата необходимо найти напряженность поля в этой точке. Согласно принципу суперпозиции полей, напряженность в точке пересечения диагоналей квадрата равна:
в точке пересечения диагоналей квадрата необходимо найти напряженность поля в этой точке. Согласно принципу суперпозиции полей, напряженность в точке пересечения диагоналей квадрата равна:  , где
, где  – напряженности полей, создаваемых точечными зарядами
– напряженности полей, создаваемых точечными зарядами  ,
,  ,
, 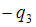 ,
,  в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов.
в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов.
 Величина напряженности поля точечного заряда определяется по формуле
Величина напряженности поля точечного заряда определяется по формуле  , где
, где  электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов
электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов  равны, т.е.
равны, т.е.  , а
, а  образует диагональ квадрата со стороной 2Е. Модуль напряженности результирующего поля в центре квадрата
образует диагональ квадрата со стороной 2Е. Модуль напряженности результирующего поля в центре квадрата  . Учитывая связь напряженности поля и потенциала, градиент потенциала в центре квадрата равен
. Учитывая связь напряженности поля и потенциала, градиент потенциала в центре квадрата равен  и направлен вправо.
и направлен вправо.
Задание №24
Не нашли, что искали? Воспользуйтесь поиском: