
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Первый закон термодинамики
Первый закон (первое начало) термодинамики - это, фактически, закон сохранения энергии. Он утверждает, что
Энергия изолированной системы постоянна. В неизолированной системе энергия может изменяться за счет: а) совершения работы над окружающей средой; б) теплообмена с окружающей средой.
Для описания этих изменений вводят функцию состояния - внутреннюю энергию U и две функции перехода - теплоту Q и работу A. Математическая формулировка первого закона:
dU =  Q -
Q -  A (дифференциальная форма) (2.1)
A (дифференциальная форма) (2.1)
 U = Q - A (интегральная форма) (2.2)
U = Q - A (интегральная форма) (2.2)
Буква  в уравнении (2.1) отражает тот факт, что Q и A - функции перехода и их бесконечно малое изменение не является полным дифференциалом.
в уравнении (2.1) отражает тот факт, что Q и A - функции перехода и их бесконечно малое изменение не является полным дифференциалом.
В уравнениях (2.1) и (2.2) знаки теплоты и работы выбраны следующим образом. Теплота считается положительной, если она передается системе. Напротив, работа считается положительной, если она совершается системой над окружающей средой.
Существуют разные виды работы: механическая, электрическая, магнитная, поверхностная и др. Бесконечно малую работу любого вида можно представить как произведение обобщенной силы на приращение обобщенной координаты, например:
 A мех = p. dV;
A мех = p. dV;  A эл =
A эл =  . dе;
. dе;  A пов =
A пов =  . dW (2.3)
. dW (2.3)
( - электрический потенциал, e - заряд,
- электрический потенциал, e - заряд,  - поверхностное натяжение, W - площадь поверхности). С учетом (2.3), дифференциальное выражение первого закона можно представить в виде:
- поверхностное натяжение, W - площадь поверхности). С учетом (2.3), дифференциальное выражение первого закона можно представить в виде:
dU =  Q - p. dV
Q - p. dV 
 A немех (2.4)
A немех (2.4)
В дальнейшем изложении немеханическими видами работы мы будем, по умолчанию, пренебрегать.
Механическую работу, производимую при расширении против внешнего давления p ex, рассчитывают по формуле:
A =  (2.5)
(2.5)
Если процесс расширения обратим, то внешнее давление отличается от давления системы (например, газа) на бесконечно малую величину: p ex = p in - dp и в формулу (2.5) можно подставлять давление самой системы, которое определяется по уравнению состояния.
Проще всего рассчитывать работу, совершаемую идеальным газом, для которого известно уравнение состояния p = nRT / V (табл. 1).
Таблица 1. Работа идеального газа в некоторых процессах расширения V 1  V 2:
V 2:
| Процесс | A |
| Расширение в вакуум | |
| Расширение против постоянного внешнего давления p | p (V 2- V 1) |
| Изотермическое обратимое расширение | nRT ln(V 2/ V 1) |
| Адиабатическое обратимое расширение | nC V(T 1- T 2) |
При обратимом процессе совершаемая работа максимальна.
Теплота может переходить в систему при нагревании. Для расчета теплоты используют понятие теплоемкости, которая определяется следующим образом:
C =  (2.6)
(2.6)
Если нагревание происходит при постоянном объеме или давлении, то теплоемкость обозначают соответствующим нижним индексом:
C V =  ; Cp =
; Cp =  . (2.7)
. (2.7)
Из определения (2.6) следует, что конечную теплоту, полученную системой при нагревании, можно рассчитать как интеграл:
Q =  (2.8)
(2.8)
Теплоемкость - экспериментально измеряемая экстенсивная величина. В термодинамических таблицах приведены значения теплоемкости при 298 К и коэффициенты, описывающие ее зависимость от температуры. Для некоторых веществ теплоемкость можно также оценить теоретически методами статистической термодинамики (гл. 12). Так, при комнатной температуре для одноатомных идеальных газов мольная теплоемкость C V = 3/2 R, для двухатомных газов C V = 5/2 R.
Теплоемкость определяется через теплоту, переданную системе, однако ее можно связать и с изменением внутренней энергии. Так, при постоянном объеме механическая работа не совершается и теплота равна изменению внутренней энергии:  Q V = dU, поэтому
Q V = dU, поэтому
C V =  . (2.9)
. (2.9)
При постоянном давлении теплота равна изменению другой функции состояния, которую называют энтальпией:
 Qp = dU + pdV = d (U + pV) = dH, (2.10)
Qp = dU + pdV = d (U + pV) = dH, (2.10)
где H = U + pV - энтальпия системы. Из (2.10) следует, что теплоемкость C p определяет зависимость энтальпии от температуры.
C p =  . (2.11)
. (2.11)
Из соотношения между внутренней энергией и энтальпией следует, что для моля идеального газа
C p - C V = R. (2.12)
Внутреннюю энергию можно рассматривать, как функцию температуры и объема:
 (2.13)
(2.13)
Для идеального газа экспериментально обнаружено, что внутренняя энергия не зависит от объема,  , откуда можно получить калорическое уравнение состояния:
, откуда можно получить калорическое уравнение состояния:
dU = C V dT,
 (2.14)
(2.14)
В изотермических процессах с участием идеального газа внутренняя энергия не изменяется, и работа расширения происходит только за счет поглощаемой теплоты.
Возможен и совсем иной процесс. Если в течение процесса отсутствует теплообмен с окружающей средой ( Q = 0), то такой процесс называют адиабатическим. В адиабатическом процессе работа может совершаться только за счет убыли внутренней энергии. Работа обратимого адиабатического расширения идеального газа:
Q = 0), то такой процесс называют адиабатическим. В адиабатическом процессе работа может совершаться только за счет убыли внутренней энергии. Работа обратимого адиабатического расширения идеального газа:
A = -  U = nC V (T 1- T 2) (2.15)
U = nC V (T 1- T 2) (2.15)
(n - число молей, C V - мольная теплоемкость). Эту работу можно также выразить через начальные и конечные давление и объем:
A =  (2.16)
(2.16)
где  = C p / C V.
= C p / C V.
При обратимом адиабатическом расширении идеального газа давление и объем связаны соотношением (уравнением адиабаты):
pV  = const. (2.17)
= const. (2.17)
В уравнении (2.17) важны два момента: во-первых, это уравнение процесса, а не уравнение состояния; во-вторых, оно справедливо только для обратимого адиабатического процесса. Это же уравнение можно записать в эквивалентном виде:
TV  -1 = const, (2.18)
-1 = const, (2.18)
T  p 1-
p 1-  = const. (2.19)
= const. (2.19)
ПРИМЕРЫ
Пример 2-1. Рассчитайте изменение внутренней энергии гелия (одноатомный идеальный газ) при изобарном расширении от 5 до 10 л под давлением 196 кПа.
Решение. p 1 = p 2 = 196 кПа, V 1 = 5 л, V 2 = 10 л. Начальная и конечная температуры: T 1 = p 1 V 1 / nR, T 2 = p 2 V 2 / nR. Изменение внутренней энергии идеального газа определяется только начальной и конечной температурой (C V = 3/2 nR - идеальный одноатомный газ):
 U = C V (T 2- T 1) = 3/2 nR (T 2- T 1) = 3/2 (p 2 V 2 - p 1 V 1) = 3/2
U = C V (T 2- T 1) = 3/2 nR (T 2- T 1) = 3/2 (p 2 V 2 - p 1 V 1) = 3/2  (196. 103)
(196. 103)  (10-5). 10-3 =
(10-5). 10-3 =
= 1470 Дж.
Ответ. 1470 Дж.
Пример 2-2. Используя первый закон и определение теплоемкости, найдите разность изобарной и изохорной теплоемкостей для произвольной термодинамической системы.
Решение. В определение теплоемкости (2.6) подставим дифференциальное представление первого закона (2.1) и используем соотношение (2.13) для внутренней энергии как функции температуры и объема:

Отсюда при постоянном давлении получаем:

Пример 2-3. Один моль ксенона, находящийся при 25 оС и 2 атм, расширяется адиабатически: а) обратимо до 1 атм, б) против давления 1 атм. Какой будет конечная температура в каждом случае?
Решение. а) Исходный объем ксенона (n = 1):
V 1 = nRT 1 / p 1 = 0.082. 298 / 2 = 12.2 л.
Конечный объем можно найти из уравнения адиабаты (для одноатомного идеального газа  = Cp / C V = 5/3):
= Cp / C V = 5/3):
p 1 V 15/3 = p 2 V 25/3
V 2 = V 1 . (p 1/ p 2)3/5 = 12.2 . 23/5 = 18.5 л.
Конечную температуру находим по уравнению состояния идеального газа (p 2 = 1 атм):
T 2 = p 2 V 2 / nR = 18.5 / 0.082 = 225 К.
б) При необратимом расширении против постоянного внешнего давления уравнение адиабаты неприменимо, поэтому надо воспользоваться первым законом термодинамики. Работа совершается за счет убыли внутренней энергии:
A = -  U = nC V(T 1- T 2),
U = nC V(T 1- T 2),
где n = 1, C V = 3/2 R (одноатомный идеальный газ). Работа расширения против постоянного внешнего давления p 2 равна:
A = p 2 (V 2- V 1) = nRT 2 - p 2 V 1.
Приравнивая последние два выражения, находим температуру T 2:
T 2 = (nC V T 1 + p 2 V 1) / (nC V + nR) = 238 К.
Температура выше, чем при обратимом расширении, т.к. в обратимом случае совершается бМльшая работа, расходуется больше внутренней энергии и температура понижается на большую величину.
Ответ. а) 225 К; б) 238 К.
Пример 2-4. Один моль водяных паров обратимо и изотермически сконденсировали в жидкость при 100 оС. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения воды при 100 оС равна 2260 Дж/г.
Решение. В процессе
H2O(г)  H2O(ж)
H2O(ж)
произошло обратимое сжатие газа при постоянном давлении p = 1 атм от объема V 1 = nRT / p = 0.082. 373 = 30.6 л до объема одного моля жидкой воды V 2 ~ 0.018 л. Работа сжатия при постоянном давлении равна:
A = p (V 2- V 1) 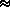 - pV 1 = -101.3 кПа
- pV 1 = -101.3 кПа  30.6 л = -3100 Дж.
30.6 л = -3100 Дж.
При испарении одного моля воды затрачивается теплота 2260 Дж/г  18 г = 40700 Дж, поэтому при конденсации одного моля воды эта теплота, напротив, выделяется в окружающую среду:
18 г = 40700 Дж, поэтому при конденсации одного моля воды эта теплота, напротив, выделяется в окружающую среду:
Q = -40700 Дж.
Изменение внутренней энергии можно рассчитать по первому закону:
 U = Q - A = -40700 - (-3100) = -37600 Дж,
U = Q - A = -40700 - (-3100) = -37600 Дж,
а изменение энтальпии - через изменение внутренней энергии:
 H =
H =  U +
U +  (pV) =
(pV) =  U + p
U + p  V =
V =  U + A = Q = -40700 Дж.
U + A = Q = -40700 Дж.
Изменение энтальпии равно теплоте, т.к. процесс происходит при постоянном давлении.
Ответ. A = -3100 Дж, Q =  H = -40700 Дж,
H = -40700 Дж,  U = -37600 Дж.
U = -37600 Дж.
ЗАДАЧИ
2-1. Газ, расширяясь от 10 до 16 л при постоянном давлении 101.3 кПа, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа.
2-2. Определите изменение внутренней энергии, количество теплоты и работу, совершаемую при обратимом изотермическом расширении азота от 0.5 до 4 м3 (начальные условия: температура 26.8 оС, давление 93.2 кПа).
2-3. Один моль идеального газа, взятого при 25 oC и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту,  U и
U и  H.
H.
2-4. Рассчитайте изменение энтальпии кислорода (идеальный газ) при изобарном расширении от 80 до 200 л при нормальном атмосферном давлении.
2-5. Какое количество теплоты необходимо для повышения температуры 16 г кислорода от 300 до 500 К при давлении 1 атм? Как при этом изменится внутренняя энергия?
2-6. Объясните, почему для любой термодинамической системы C p > C V.
2-7. Чайник, содержащий 1 кг кипящей воды, нагревают до полного испарения при нормальном давлении. Определите A, Q,  U,
U,  H для этого процесса. Мольная теплота испарения воды 40.6 кДж/моль.
H для этого процесса. Мольная теплота испарения воды 40.6 кДж/моль.
2-8. Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10 л до 1 л, если начальные температура и давление равны 26.8 оС и 101.3 кПа, соответственно.
2-9. Три моля идеального одноатомного газа (C V = 3.0 кал/(моль. К)), находящегося при T 1 = 350 K и P 1 = 5 атм, обратимо и адиабатически расширяются до давления P 2 = 1 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии и энтальпии в этом процессе.
2-10. Система содержит 0.5 моль идеального одноатомного газа (C V = 3.0 кал/(моль. К)) при P 1 = 10 атм и V 1 = 1 л. Газ расширяется обратимо и адиабатически до давления P 2 = 1 атм. Рассчитайте начальную и конечную температуру, конечный объем, совершенную работу, а также изменение внутренней энергии и энтальпии в этом процессе. Рассчитайте эти величины для соответствующего изотермического процесса.
2-11. Рассчитайте количество теплоты, необходимое для нагревания воздуха в квартире общим объемом 600 м3 от 20 оС до 25 оС. Примите, что воздух - это идеальный двухатомный газ, а давление при исходной температуре нормальное. Найдите  U и
U и  H для процесса нагревания воздуха.
H для процесса нагревания воздуха.
2-12. Человеческий организм в среднем выделяет 104 кДж в день благодаря метаболическим процессам. Основной механизм потери этой энергии - испарение воды. Какую массу воды должен ежедневно испарять организм для поддержания постоянной температуры? Удельная теплота испарения воды - 2260 Дж/г. На сколько градусов повысилась бы температура тела, если бы организм был изолированной системой? Примите, что средняя масса человека - 65 кг, а теплоемкость равна теплоемкости жидкой воды.
2-13. Один моль паров брома обратимо и изотермически сконденсировали в жидкость при 59 оС. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения брома при 59 оС равна 184.1 Дж/г.
2-14. Один моль идеального одноатомного газа вступает в следующий замкнутый цикл:

Процесс 1  2 - изотермический, 3
2 - изотермический, 3  1 - адиабатический. Рассчитайте объемы состояний 2 и 3, а также температуры состояний 1, 2 и 3, считая стадии 1
1 - адиабатический. Рассчитайте объемы состояний 2 и 3, а также температуры состояний 1, 2 и 3, считая стадии 1  2 и 3
2 и 3  1 обратимыми. Рассчитайте
1 обратимыми. Рассчитайте  U и
U и  H для каждой стадии.
H для каждой стадии.
2-15. Придумайте циклический процесс с идеальным газом, состоящий из четырех стадий. Изобразите этот процесс в координатах p - V. Рассчитайте полное изменение внутренней энергии, а также теплоту и совершенную газом работу.
2-16. Один моль фтороуглерода расширяется обратимо и адиабатически вдвое по объему, при этом температура падает от 298.15 до 248.44 К. Чему равно значение C V?
2-17. Докажите соотношение (2.16) для работы обратимого адиабатического процесса.
2-18. Один моль метана, взятый при 25 оС и 1 атм, нагрет при постоянном давлении до удвоения объема. Мольная теплоемкость метана дается выражением:
Cp = 5.34 + 0.0115. T кал/(моль. К).
Рассчитайте  U и
U и  H для этого процесса. Метан можно считать идеальным газом.
H для этого процесса. Метан можно считать идеальным газом.
2-19. Выведите уравнение для обратимого адиабатического сжатия неидеального газа, если уравнение состояния одного моля газа имеет вид:
p (V - b) = RT.
2-20*. Используя уравнение состояния и первый закон термодинамики, выведите уравнение адиабаты для газа Ван-дер-Ваальса.
Термохимия
Термохимия изучает тепловые эффекты химических реакций. Во многих случаях эти реакции протекают при постоянном объеме или постоянном давлении. Из первого закона термодинамики следует, что при этих условиях теплота является функцией состояния. При постоянном объеме теплота равна изменению внутренней энергии:
 ,
,  , (3.1)
, (3.1)
а при постоянном давлении - изменению энтальпии:
 ,
,  . (3.2)
. (3.2)
Эти равенства в применении к химическим реакциям составляют суть закона Гесса:
Тепловой эффект химической реакции, протекающей при постоянном давлении или постоянном объеме, не зависит от пути реакции, а определяется только состоянием реагентов и продуктов реакции.
Другими словами, тепловой эффект химической реакции равен изменению функции состояния.
В термохимии, в отличие от других приложений термодинамики, теплота считается положительной, если она выделяется в окружающую среду, т.е. если  H < 0 или
H < 0 или  U < 0. Под тепловым эффектом химической реакции понимают значение
U < 0. Под тепловым эффектом химической реакции понимают значение  H (которое называют просто "энтальпией реакции") или
H (которое называют просто "энтальпией реакции") или  U реакции.
U реакции.
Если реакция протекает в растворе или в твердой фазе, где изменение объема незначительно, то
 H =
H =  U +
U +  (pV)
(pV) 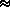
 U. (3.3)
U. (3.3)
Если же в реакции участвуют идеальные газы, то при постоянной температуре
 H =
H =  U +
U +  (pV) =
(pV) =  U +
U +  n . RT, (3.4)
n . RT, (3.4)
где  n - изменение числа молей газов в реакции.
n - изменение числа молей газов в реакции.
Для того, чтобы облегчить сравнение энтальпий различных реакций, используют понятие "стандартного состояния". Стандартное состояние - это состояние чистого вещества при давлении 1 бар (= 105 Па) и заданной температуре. Для газов - это гипотетическое состояние при давлении 1 бар, обладающее свойствами бесконечно разреженного газа.Энтальпию реакции между веществами, находящимися в стандартных состояниях при температуре T, обозначают  (r означает "reaction"). В термохимических уравнениях указывают не только формулы веществ, но и их агрегатные состояния или кристаллические модификации.
(r означает "reaction"). В термохимических уравнениях указывают не только формулы веществ, но и их агрегатные состояния или кристаллические модификации.
Из закона Гесса вытекают важные следствия, которые позволяют рассчитывать энтальпии химических реакций.
Следствие 1. Стандартная энтальпия химической реакции
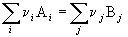
равна разности стандартных энтальпий образования продуктов реакции и реагентов (с учетом стехиометрических коэффициентов):
 (3.5)
(3.5)
Стандартной энтальпией (теплотой) образования вещества 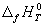 (f означает "formation") при заданной температуре называют энтальпию реакции образования одного моля этого вещества из элементов, находящихся в наиболее устойчивом стандартном состоянии. Согласно этому определению, энтальпия образования наиболее устойчивых простых веществ в стандартном состоянии равна 0 при любой температуре. Стандартные энтальпии образования веществ при температуре 298 К приведены в справочниках.
(f означает "formation") при заданной температуре называют энтальпию реакции образования одного моля этого вещества из элементов, находящихся в наиболее устойчивом стандартном состоянии. Согласно этому определению, энтальпия образования наиболее устойчивых простых веществ в стандартном состоянии равна 0 при любой температуре. Стандартные энтальпии образования веществ при температуре 298 К приведены в справочниках.
Понятия "энтальпия образования" используют не только для обычных веществ, но и для ионов в растворе. При этом за точку отсчета принят ион H+, для которого стандартная энтальпия образования в водном растворе полагается равной нулю: 
Следствие 2. Стандартная энтальпия химической реакции
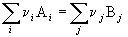
равна разности энтальпий сгорания реагентов и продуктов реакции (с учетом стехиометрических коэффициентов):
 (3.6)
(3.6)
(c означает "combustion"). Стандартной энтальпией (теплотой) сгорания вещества называют энтальпию реакции полного окисления одного моля вещества. Это следствие обычно используют для расчета тепловых эффектов органических реакций.
Следствие 3. Энтальпия химической реакции равна разности энергий разрываемых и образующихся химических связей.
Энергией связи A- B называют энергию, необходимую для разрыва связи и разведения образующихся частиц на бесконечное расстояние:
AB(г)  A(г) + B(г).
A(г) + B(г).
Энергия связи всегда положительна.
Большинство термохимических данных в справочниках приведено при температуре 298 К. Для расчета тепловых эффектов при других температурах используют уравнение Кирхгофа:
 (дифференциальная форма) (3.7)
(дифференциальная форма) (3.7)
 (интегральная форма) (3.8)
(интегральная форма) (3.8)
где  Cp - разность изобарных теплоемкостей продуктов реакции и исходных веществ. Если разница T 2 - T 1 невелика, то можно принять
Cp - разность изобарных теплоемкостей продуктов реакции и исходных веществ. Если разница T 2 - T 1 невелика, то можно принять  Cp = const. При большой разнице температур необходимо использовать температурную зависимость
Cp = const. При большой разнице температур необходимо использовать температурную зависимость  Cp (T) типа:
Cp (T) типа:
 , (3.9)
, (3.9)
где коэффициенты a, b, c и т.д. для отдельных веществ берут из справочника, а знак  обозначает разность между продуктами и реагентами (с учетом коэффициентов).
обозначает разность между продуктами и реагентами (с учетом коэффициентов).
ПРИМЕРЫ
Пример 3-1. Стандартные энтальпии образования жидкой и газообразной воды при 298 К равны -285.8 и -241.8 кДж/моль, соответственно. Рассчитайте энтальпию испарения воды при этой температуре.
Решение. Энтальпии образования соответствуют следующим реакциям:
H2(г) + ЅO2(г) = H2O(ж),  H 10 = -285.8;
H 10 = -285.8;
H2(г) + ЅO2(г) = H2O(г),  H 20 = -241.8.
H 20 = -241.8.
Вторую реакцию можно провести в две стадии: сначала сжечь водород с образованием жидкой воды по первой реакции, а затем испарить воду:
H2O(ж) = H2O(г),  H 0исп =?
H 0исп =?
Тогда, согласно закону Гесса,
 H 10 +
H 10 +  H 0исп =
H 0исп =  H 20,
H 20,
откуда  H 0исп = -241.8 - (-285.8) = 44.0 кДж/моль.
H 0исп = -241.8 - (-285.8) = 44.0 кДж/моль.
Ответ. 44.0 кДж/моль.
Пример 3-2. Рассчитайте энтальпию реакции
6C(г) + 6H(г) = C6H6(г)
а) по энтальпиям образования; б) по энергиям связи, в предположении, что двойные связи в молекуле C6H6 фиксированы.
Решение. а) Энтальпии образования (в кДж/моль) находим в справочнике (например, P.W.Atkins, Physical Chemistry, 5th edition, pp. C9-C15):  fH 0(C6H6(г)) = 82.93,
fH 0(C6H6(г)) = 82.93,  fH 0(C(г)) = 716.68,
fH 0(C(г)) = 716.68,  fH 0(H(г)) = 217.97. Энтальпия реакции равна:
fH 0(H(г)) = 217.97. Энтальпия реакции равна:
 rH 0 = 82.93 - 6
rH 0 = 82.93 - 6  716.68 - 6
716.68 - 6  217.97 = -5525 кДж/моль.
217.97 = -5525 кДж/моль.
б) В данной реакции химические связи не разрываются, а только образуются. В приближении фиксированных двойных связей молекула C6H6 содержит 6 связей C- H, 3 связи C- C и 3 связи C=C. Энергии связей (в кДж/моль) (P.W.Atkins, Physical Chemistry, 5th edition, p. C7): E (C- H) = 412, E (C- C) = 348, E (C=C) = 612. Энтальпия реакции равна:
 rH 0 = -(6
rH 0 = -(6  412 + 3
412 + 3  348 + 3
348 + 3  612) = -5352 кДж/моль.
612) = -5352 кДж/моль.
Разница с точным результатом -5525 кДж/моль обусловлена тем, что в молекуле бензола нет одинарных связей C- C и двойных связей C=C, а есть 6 ароматических связей C  C.
C.
Ответ. а) -5525 кДж/моль; б) -5352 кДж/моль.
Пример 3-3. Пользуясь справочными данными, рассчитайте энтальпию реакции
3Cu(тв) + 8HNO3(aq) = 3Cu(NO3)2(aq) + 2NO(г) + 4H2O(ж)
при 298 К.
Решение. Сокращенное ионное уравнение реакции имеет вид:
3Cu(тв) + 8H+(aq) + 2NO3-(aq) = 3Cu2+(aq) + 2NO(г) + 4H2O(ж).
По закону Гесса, энтальпия реакции равна:
 rH 0 = 4
rH 0 = 4  fH 0(H2O(ж)) + 2
fH 0(H2O(ж)) + 2  fH 0(NO(г)) + 3
fH 0(NO(г)) + 3  fH 0(Cu2+(aq)) - 2
fH 0(Cu2+(aq)) - 2  fH 0(NO3-(aq))
fH 0(NO3-(aq))
(энтальпии образования меди и иона H+ равны, по определению, 0). Подставляя значения энтальпий образования (P.W.Atkins, Physical Chemistry, 5th edition, pp. C9-C15), находим:
 rH 0 = 4
rH 0 = 4  (-285.8) + 2
(-285.8) + 2  90.25 + 3
90.25 + 3  64.77 - 2
64.77 - 2  (-205.0) = -358.4 кДж
(-205.0) = -358.4 кДж
(в расчете на три моля меди).
Ответ. -358.4 кДж.
Пример 3-4. Рассчитайте энтальпию сгорания метана при 1000 К, если даны энтальпии образования при 298 К:  fH 0(CH4) = -17.9 ккал/моль,
fH 0(CH4) = -17.9 ккал/моль,  fH 0(CO2) = -94.1 ккал/моль,
fH 0(CO2) = -94.1 ккал/моль,  fH 0(H2O(г)) = -57.8 ккал/моль. Теплоемкости газов (в кал/(моль. К)) в интервале от 298 до 1000 К равны:
fH 0(H2O(г)) = -57.8 ккал/моль. Теплоемкости газов (в кал/(моль. К)) в интервале от 298 до 1000 К равны:
Cp (CH4) = 3.422 + 0.0178. T, Cp (O2) = 6.095 + 0.0033. T,
Cp (CO2) = 6.396 + 0.0102. T, Cp (H2O(г)) = 7.188 + 0.0024. T.
Решение. Энтальпия реакции сгорания метана
CH4(г) + 2O2(г) = CO2(г) + 2H2O(г)
при 298 К равна:
 = -94.1 + 2
= -94.1 + 2  (-57.8) - (-17.9) = -191.8 ккал/моль.
(-57.8) - (-17.9) = -191.8 ккал/моль.
Найдем разность теплоемкостей как функцию температуры:
 Cp = Cp (CO2) + 2
Cp = Cp (CO2) + 2  Cp (H2O(г)) - Cp (CH4) - 2
Cp (H2O(г)) - Cp (CH4) - 2  Cp (O2) =
Cp (O2) =
= 5.16 - 0.0094 T (кал/(моль. К)).
Энтальпию реакции при 1000 К рассчитаем по уравнению Кирхгофа:
 =
=  +
+  = -191800 + 5.16
= -191800 + 5.16 
 (1000-298) - 0.0094
(1000-298) - 0.0094  (10002-2982)/2 = -192500 кал/моль.
(10002-2982)/2 = -192500 кал/моль.
Ответ. -192.5 ккал/моль.
ЗАДАЧИ
3-1. Сколько тепла потребуется на перевод 500 г Al (т.пл. 658 оС,  H 0пл = 92.4 кал/г), взятого при комнатной температуре, в расплавленное состояние, если Cp (Alтв) = 0.183 + 1.096
H 0пл = 92.4 кал/г), взятого при комнатной температуре, в расплавленное состояние, если Cp (Alтв) = 0.183 + 1.096  10-4 T кал/(г
10-4 T кал/(г  К)?
К)?
3-2. Стандартная энтальпия реакции CaCO3(тв) = CaO(тв) + CO2(г), протекающей в открытом сосуде при температуре 1000 К, равна 169 кДж/моль. Чему равна теплота этой реакции, протекающей при той же температуре, но в закрытом сосуде?
3-3. Рассчитайте стандартную внутреннюю энергию образования жидкого бензола при 298 К, если стандартная энтальпия его образования равна 49.0 кДж/моль.
3-4. Рассчитайте энтальпию образования N2O5(г) при T = 298 К на основании следующих данных:
2NO(г) + O2(г) = 2NO2(г),  H 10 = -114.2 кДж/моль,
H 10 = -114.2 кДж/моль,
4NO2(г) + O2(г) = 2N2O5(г),  H 20 = -110.2 кДж/моль,
H 20 = -110.2 кДж/моль,
N2(г) + O2(г) = 2NO(г),  H 30 = 182.6 кДж/моль.
H 30 = 182.6 кДж/моль.
3-5. Энтальпии сгорания  -глюкозы,
-глюкозы,  -фруктозы и сахарозы при 25 оС равны -2802,
-фруктозы и сахарозы при 25 оС равны -2802,
-2810 и -5644 кДж/моль, соответственно. Рассчитайте теплоту гидролиза сахарозы.
3-6. Определите энтальпию образования диборана B2H6(г) при T = 298 К из следующих данных:
B2H6(г) + 3O2(г) = B2O3(тв) + 3H2O(г),  H 10 = -2035.6 кДж/моль,
H 10 = -2035.6 кДж/моль,
2B(тв) + 3/2 O2(г) = B2O3(тв),  H 20 = -1273.5 кДж/моль,
H 20 = -1273.5 кДж/моль,
H2(г) + 1/2 O2(г) = H2O(г),  H 30 = -241.8 кДж/моль.
H 30 = -241.8 кДж/моль.
3-7. Рассчитайте теплоту образования сульфата цинка из простых веществ при T = 298 К на основании следующих данных:
ZnS = Zn + S,  H 10 = 200.5 кДж/моль,
H 10 = 200.5 кДж/моль,
2ZnS + 3O2 = 2ZnO + 2SO2,  H 20 = -893.5 кДж,
H 20 = -893.5 кДж,
2SO2 + O2 = 2SO3,  H 30 = -198.2 кДж/моль,
H 30 = -198.2 кДж/моль,
ZnSO4 = ZnO + SO3,  H 40 = 235.0 кДж/моль.
H 40 = 235.0 кДж/моль.
3-8. Найдите  rH 0298 для реакции
rH 0298 для реакции
CH4 + Cl2 = CH3Cl(г) + HCl(г),
если известны теплоты сгорания метана ( cH 0(CH4) = -890.6 кДж/моль), хлорметана (
cH 0(CH4) = -890.6 кДж/моль), хлорметана ( cH 0(CH3Cl) = -689.8 кДж/моль), водорода (
cH 0(CH3Cl) = -689.8 кДж/моль), водорода ( cH 0(H2) = -285.8 кДж/моль) и теплота образования HCl (
cH 0(H2) = -285.8 кДж/моль) и теплота образования HCl ( fH 0(HCl) = -92.3 кДж/моль)).
fH 0(HCl) = -92.3 кДж/моль)).
3-9. Рассчитайте тепловой эффект реакции
NH3 + 5/4 O2 = NO + 3/2 H2O(г)
при T = 298 K, если известны следующие данные:
H2O(г) = H2O(ж),  H 10 = -44 кДж/моль,
H 10 = -44 кДж/моль,
1/2N2 + 3/2H2 = NH3,  H 20 = -46.2 кДж/моль,
H 20 = -46.2 кДж/моль,
H2 + 1/2O2 = H2O(ж),  H 30 = -285.8 кДж/моль,
H 30 = -285.8 кДж/моль,
NO = 1/2N2 + 1/2O2,  H 40 = -91.3 кДж/моль.
H 40 = -91.3 кДж/моль.
3-10. При взаимодействии 10 г металлического натрия с водой  rH 298 = -79.91 кДж, а при взаимодействии 20 г оксида натрия с водой
rH 298 = -79.91 кДж, а при взаимодействии 20 г оксида натрия с водой  rH 298 = -76.76 кДж. Вода берется в большом избытке. Рассчитайте теплоту образования оксида натрия
rH 298 = -76.76 кДж. Вода берется в большом избытке. Рассчитайте теплоту образования оксида натрия  fH 0298(Na2O), если
fH 0298(Na2O), если  fH 0298(H2Oж) = -285.8 кДж/моль.
fH 0298(H2Oж) = -285.8 кДж/моль.
3-11. Энергия связи в молекуле H2 равна 432.1 кДж/моль, а энергия связи в молекуле N2 равна 945.3 кДж/моль. Какова энтальпия атомизации аммиака, если энтальпия образования аммиака равна -46.2 кДж/моль?
3-12. Рассчитайте стандартный тепловой эффект реакции нейтрализации
NaOH + HCl = NaCl + H2O,
протекающей в водном растворе при 298 К.
3-13. Рассчитайте стандартный тепловой эффект реакции
CaSO4(тв) + Na2CO3(aq) = CaCO3(тв) + Na2SO4(aq)
при 298 К.
3-14. Напишите уравнение Кирхгофа для реакции, протекающей при постоянном объеме.
3-15. Зависимость теплового эффекта реакции CH3OH(г) + 3/2O2 = CO2 + 2H2O(г) от температуры выражается уравнением:
 (Дж) =
(Дж) = 
Рассчитайте изменение теплоемкости  Cp для этой реакции при 500 К.
Cp для этой реакции при 500 К.
3-16. Стандартная энтальпия образования Al2O3(тв) при 298 К равна -1675 кДж/моль. Рассчитайте стандартную энтальпию образования Al2O3(тв) при 800 К, если даны мольные теплоемкости (в Дж/(моль. К)):
Cp (Al) = 20.67 + 12.39. 10-3 T, Cp (O2) = 31.46 + 3.39. 10-3 T - 3.77. 105 T -2,
Cp (Al2O3) = 114.56 + 12.89. 10-3 T - 34.31. 105 T -2.
3-17. Энтальпия диссоциации карбоната кальция при 900 оС и давлении 1 атм равна 178 кДж/моль. Выведите уравнение зависимости энтальпии реакции от температуры и рассчитайте количество теплоты, поглощенное при разложении 1 кг карбоната кальция при 1000 оС и 1 атм, если даны мольные теплоемкости (в Дж/(моль. К)):
Cp (СaCO3(тв)) = 104.5 + 21.92. 10-3 T - 25.94. 105 T -2,
Cp (СaO(тв)) = 49.63 + 4.52. 10-3 T - 6.95. 105 T -2,
Cp (CO2(г)) = 44.14 + 9.04. 10-3 T - 8.53. 105 T -2.
Не нашли, что искали? Воспользуйтесь поиском: