Химическое равновесие

Химическим равновесием называется такое состояние обратимой химической реакции

aA + bB = cC + dD,

при котором с течением времени не происходит изменения концентраций реагирующих веществ в реакционной смеси. Состояние химического равновесия характеризуется константой химического равновесия:

, (9.1)

где C_i – концентрации компонентов в равновесной идеальной смеси.

Константа равновесия может быть выражена также через равновесные мольные доли X_i компонентов:

. (9.2)

Для реакций, протекающих в газовой фазе, константу равновесия удобно выражать через равновесные парциальные давления P_i компонентов:

. (9.3)

Для идеальных газов P_i = C_iRT и P_i = X_iP, где P – общее давление, поэтому K_P, K_C и K_X связаны следующим соотношением:

K_P = K_C (RT) ^c+d–a–b = K_XP ^c+d–a–b. (9.4)

Константа равновесия связана с _rG^o химической реакции:

(9.5)

(9.6)

Изменение _rG или _rF в химической реакции при заданных (не обязательно равновесных) парциальных давлениях P_i или концентрациях C_i компонентов можно рассчитать по уравнению изотермы химической реакции (изотермы Вант-Гоффа):

. (9.7)

. (9.8)

Согласно принципу Ле Шателье, если на систему, находящуюся в равновесии, оказать внешнее воздействие, то равновесие сместится так, чтобы уменьшить эффект внешнего воздействия. Так, повышение давления сдвигает равновесие в сторону уменьшения количества молекул газа. Добавление в равновесную смесь какого-либо компонента реакции сдвигает равновесие в сторону уменьшения количества этого компонента. Повышение (или понижение) температуры сдвигает равновесие в сторону реакции, протекающей с поглощением (выделением) теплоты.

Количественно зависимость константы равновесия от температуры описывается уравнением изобары химической реакции (изобары Вант-Гоффа)

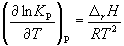(9.9)

и изохоры химической реакции (изохоры Вант-Гоффа)

. (9.10)

Интегрирование уравнения (9.9) в предположении, что _rH реакции не зависит от температуры (что справедливо в узких интервалах температур), дает:

(9.11)

(9.12)

где C – константа интегрирования. Таким образом, зависимость ln K_P от 1/Т должна быть линейной, а наклон прямой равен – _rH /R.

Интегрирование в пределах K₁, K₂, и T_1, T₂ дает:

(9.13)

(9.14)

По этому уравнению, зная константы равновесия при двух разных температурах, можно рассчитать _rH реакции. Соответственно, зная _rH реакции и константу равновесия при одной температуре, можно рассчитать константу равновесия при другой температуре.

ПРИМЕРЫ

Пример 9-1. Рассчитать константу равновесия для реакции

CO(г) + 2H₂(г) = CH₃OH(г)

при 500 K. _fG^o для CO(г) и CH₃OH(г) при 500 К равны –155.41 кДж^. моль^–1 и –134.20 кДж^. моль^–1 соответственно.

Решение. G^o реакции:

_rG^o = _fG^o (CH₃OH) – _fG^o (CO) = –134.20 – (–155.41) = 21.21 кДж^. моль^–1.

= 6.09 10^–3.

Пример 9-2. Константа равновесия реакции

N₂(г) + 3H₂(г) = 2NH₃(г)

равна K_P = 1.64 10^–4 при 400^o C. Какое общее давление необходимо приложить к эквимолярной смеси N₂ и H₂, чтобы 10% N₂ превратилось в NH₃? Газы считать идеальными.

Решение. Пусть прореагировало моль N₂. Тогда

	N2(г)	+	3H2(г)	=	2NH3(г)
Исходное количество
Равновесное количество	1–		1–3		2 (Всего: 2–2 )
Равновесная мольная доля:

Следовательно, K_X = и K_P = K_X^. P^–2 = .

Подставляя = 0.1 в полученную формулу, имеем

1.64 10^–4 = 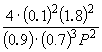, откуда P = 51.2 атм.

Пример 9-3. Константа равновесия реакции

CO(г) + 2H₂(г) = CH₃OH(г)

при 500 K равна K_P = 6.09 10^–3. Реакционная смесь, состоящая из 1 моль CO, 2 моль H₂ и 1 моль инертного газа (N₂) нагрета до 500 K и общего давления 100 атм. Рассчитать состав равновесной смеси.

Решение. Пусть прореагировало моль CO. Тогда

	CO(г)	+	2H2(г)	=	CH3OH(г)
Исходное количество:
Равновесное количество:	1–		2–2
Всего в равновесной смеси:	3–2 моль компонентов + 1 моль N2 = 4–2 моль
Равновесная мольная доля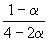

Следовательно, K_X = и K_P = K_X^. P^–2 = .

Таким образом, 6.09 10^–3 = .

Решая это уравнение, получаем = 0.732. Соответственно, мольные доли веществ в равновесной смеси равны: = 0.288, = 0.106, = 0.212 и = 0.394.

Пример 9-4. Для реакции

N₂(г) + 3H₂(г) = 2NH₃(г)

при 298 К K_P = 6.0 10⁵, а _fH^o (NH₃) = –46.1 кДж^. моль^–1. Оценить значение константы равновесия при 500 К.

Решение. Стандартная мольная энтальпия реакции равна

_rH^o = 2 _fH^o (NH₃) = –92.2 кДж^. моль^–1.

Согласно уравнению (9.14), =

= ln (6.0 10⁵) + = –1.73, откуда K₂ = 0.18.

Отметим, что константа равновесия экзотермической реакции уменьшается с ростом температуры, что соответствует принципу Ле Шателье.

ЗАДАЧИ

Указание: во всех задачах считать газы идеальными.

1. При 1273 К и общем давлении 30 атм в равновесной смеси

CO₂(г) + C(тв) = 2CO(г)

содержится 17% (по объему) CO₂. Сколько процентов CO₂ будет содержаться в газе при общем давлении 20 атм? При каком давлении в газе будет содержаться 25% CO₂?

2. При 2000^oC и общем давлении 1 атм 2% воды диссоциировано на водород и кислород. Рассчитать константу равновесия реакции

H₂O(г) = H₂(г) + 1/2O₂(г) при этих условиях.

3. Константа равновесия реакции

CO(г) + H₂O(г) = CO₂(г) + H₂(г)

при 500^oC равна K_p = 5.5. Смесь, состоящая из 1 моль CO и 5 моль H₂O, нагрели до этой температуры. Рассчитать мольную долю H₂O в равновесной смеси.

4. Константа равновесия реакции

N₂O₄(г) = 2NO₂(г)

при 25^oC равна K_p = 0.143. Рассчитать давление, которое установится в сосуде объемом 1 л, в который поместили 1 г N₂O₄ при этой температуре.

5. Сосуд объемом 3 л, содержащий 1.79 10^–2 моль I₂, нагрели до 973 K. Давление в сосуде при равновесии оказалось равно 0.49 атм. Считая газы идеальными, рассчитать константу равновесия при 973 K для реакции

I₂ (г) = 2I (г).

6. Для реакции

PCl₅(г) = PCl₃(г) + Cl₂(г)

при 250^oC _rG^o = –2508 Дж^. моль^–1. При каком общем давлении степень превращения PCl₅ в PCl₃ и Cl₂ при 250^o C составит 30%?

7. Для реакции

2HI(г) = H₂(г) + I₂(г)

константа равновесия K_P = 1.83 10^–2 при 698.6 К. Сколько граммов HI образуется при нагревании до этой температуры 10 г I₂ и 0.2 г H₂ в трехлитровом сосуде? Чему равны парциальные давления H₂, I₂ и HI?

8. Сосуд объемом 1 л, содержащий 0.341 моль PCl₅ и 0.233 моль N₂, нагрели до 250^oC. Общее давление в сосуде при равновесии оказалось равно 29.33 атм. Считая все газы идеальными, рассчитать константу равновесия при 250^oC для протекающей в сосуде реакции

PCl₅ (г) = PCl₃ (г) + Cl₂(г)

9. Константа равновесия реакции

CO(г) + 2H₂(г) = CH₃OH(г)

при 500 K равна K_P = 6.09 10^–3. Рассчитать общее давление, необходимое для получения метанола с 90% выходом, если CO и H₂ взяты в соотношении 1: 2.

10. При 25^oC _fG^o (NH₃) = –16.5 кДж^. моль^–1. Рассчитать _rG реакции образования NH₃ при парциальных давлениях N₂, H₂ и NH₃, равных 3 атм, 1 атм и 4 атм соответственно. В какую сторону реакция будет идти самопроизвольно при этих условиях?

11. Экзотермическая реакция

CO(г) + 2H₂(г) = CH₃OH(г)

находится в равновесии при 500 K и 10 бар. Если газы идеальные, как повлияют на выход метанола следующие факторы: а) повышение T; б) повышение P; в) добавление инертного газа при V = const; г) добавление инертного газа при P = const; д) добавление H₂ при P = const?

12. Константа равновесия газофазной реакции изомеризации борнеола (C₁₀H₁₇OH) в изоборнеол равна 0.106 при 503 K. Смесь 7.5 г борнеола и 14.0 г изоборнеола поместили в сосуд объемом 5 л и выдерживали при 503 K до достижения равновесия. Рассчитать мольные доли и массы борнеола и изоборнеола в равновесной смеси.

13. Равновесие в реакции

2NOCl(г) = 2NO(г) + Cl₂(г)

устанавливается при 227^oC и общем давлении 1.0 бар, когда парциальное давление NOCl равно 0.64 бар (изначально присутствовал только NOCl). Рассчитать _rG^o для реакции. При каком общем давлении парциальное давление Cl₂ будет равно 0.10 бар?

14. Рассчитать общее давление, которое необходимо приложить к смеси 3 частей H₂ и 1 части N₂, чтобы получить равновесную смесь, содержащую 10% NH₃ по объему при 400^oC. Константа равновесия для реакции

N₂(г) + 3H₂(г) = 2NH₃(г)

при 400^oC равна K = 1.60 10^–4.

15. При 250^oC и общем давлении 1 атм PCl₅ диссоциирован на 80% по реакции

PCl₅ (г) = PCl₃ (г) + Cl₂(г).

Чему будет равна степень диссоциации PCl₅, если в систему добавить N₂, чтобы парциальное давление азота было равно 0.9 атм? Общее давление поддерживается равным 1 атм.

16. При 2000^oC для реакции

N₂(г) + O₂(г) = 2NO(г)

K_p = 2.5 10^–3. В равновесной смеси N₂, O₂, NO и инертного газа при общем давлении 1 бар содержится 80% (по объему) N₂ и 16% O₂. Сколько процентов по объему составляет NO? Чему равно парциальное давление инертного газа?

17. Рассчитать стандартную энтальпию реакции, для которой константа равновесия
а) увеличивается в 2 раза, б) уменьшается в 2 раза при изменении температуры от 298 К до 308 К.

18. Оксид ртути диссоциирует по реакции

2HgO(тв) = 2Hg(г) + O₂(г).

При 420^oC давление газов равно 5.16 10⁴ Па, а при 450^oC 10.8 10⁴ Па. Рассчитать константы равновесия при этих температурах и энтальпию диссоциации на моль HgO.

19. Для реакции

Ag₂CO₃(тв) = Ag₂O(тв) + CO₂(г)

получены следующие данные по зависимости константы равновесия от температуры:

T, K
KP	3.98 10–4	1.41 10–2	1.86 10–1	1.48

Определить стандартную энтальпию реакции в этом температурном интервале.

20. Зависимость константы равновесия реакции 2C₃H₆(г) = C₂H₄(г) + C₄H₈(г) от температуры между 300 К и 600 К описывается уравнением

ln K = –1.04 –1088 /T +1.51 10⁵ /T².

Рассчитать _rG^o , _rH^o и _rS^o реакции при 400 К.

ЛИТЕРАТУРА

ГЛАВА 1

1. Полторак О.М. Термодинамика в физической химии. – М.: Высшая школа, 1991.
2. Эткинс П. Физическая химия. – М.: Мир, 1980. Т. 1, гл. 1 – 6. Atkins P. Physical Chemistry. 5^th edition. – Oxford Univ. Press, 1994, ch. 1 – 5.
3. Даниэльс Ф., Альберти Р. Физическая химия. – М.: Высшая школа, 1967, гл. 1 – 5.
4. Горшков В.И., Кузнецов И.А. Основы физической химии. – М.: Изд-во Моск. ун-та, 1993.
5. Базаров И.П. Термодинамика. – М.: Высшая школа, 1991.
6. Еремин В.В., Каргов С.И., Кузьменко Н.Е. Реальные газы. – М.: Хим. ф-т МГУ, 1998.
7. Киселева Е.В., Каретников Г.С., Кудряшов И.В. Сборник примеров и задач по физической химии. – М.: Высшая школа, 1976.
8. Картушинская А.И., Лельчук Х.А., Стромберг А.Г. Сборник задач по химической термодинамике. – М.: Высшая школа, 1973.

ГЛАВА 2

1. Даниэльс Ф., Олберти Р. Физическая химия. – М.: Мир, 1978.
2. Эткинс П. Физическая химия. – М.: Мир, 1980.
3. Горшков В.И., Кузнецов И.А. Основы физической химии. – М.: Издательство Моск. ун-та, 1993.
4. Казанская А.С., Скобло В.А. Расчеты химических равновесий. – М.: Высшая школа, 1974.
5. Киселева Е.В., Каретников Г.С., Кудряшов И.В. Сборник примеров и задач по физической химии. – М.: Высшая школа, 1976.
6. Уильямс В., Уильямс Х. Физическая химия для биологов. – М.: Мир, 1976.
7. Чанг Р. Физическая химия с приложениями к биологическим системам. – М.: Мир, 1980.
8. Alberty R.A., Silbey R.J. Physical Chemistry. Second edition. – Wiley, 1997.
9. Atkins P.W. Physical Chemistry. Fifth edition. – Oxford University Press, 1994.

Не нашли, что искали? Воспользуйтесь поиском: