Расчет изменения энтропии для различных процессов

Термодинамические расчеты изменения энтропии основаны на определении (4.6) и на свойствах частных производных энтропии по термодинамическим параметрам:

(4.8)

Последние два тождества представляют собой соотношения Максвелла (вывод см. в гл. 5).

1) Нагревание или охлаждение при постоянном давлении.

Количество теплоты, необходимое для изменения температуры системы, выражают с помощью теплоемкости: Q _обр = C_p dT.

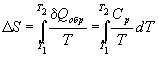(4.9)

Если теплоемкость не зависит от температуры в интервале от T ₁ до T ₂, то уравнение (4.8) можно проинтегрировать:

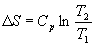. (4.10)

Если изменение температуры происходит при постоянном объеме, то в формулах (4.9) и (4.10) C_p надо заменить на C _V.

2) Изотермическое расширение или сжатие.

Для расчета энтропии в этом случае надо знать уравнение состояния системы. Расчет основан на использовании соотношения Максвелла:

(4.11)

В частности, для изотермического расширения идеального газа (p = nRT / V)

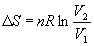(4.12)

Этот же результат можно получить, если использовать выражение для теплоты изотермического обратимого расширения идеального газа: Q _обр = nRT ln(V ₂/ V ₁) _.

3) Фазовые переходы.

При обратимом фазовом переходе температура остается постоянной, а теплота фазового перехода при постоянном давлении равна H _фп, поэтому изменение энтропии равно:

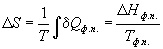(4.13)

При плавлении и кипении теплота поглощается, поэтому энтропия в этих процессах возрастает: S _тв < S _ж < S _г. При этом энтропия окружающей среды уменьшается на величину S _ф.п., поэтому изменение энтропии Вселенной равно 0, как и полагается для обратимого процесса в изолированной системе.

4) Смешение идеальных газов при постоянных температуре и давлении.

Если n ₁ молей одного газа, занимающего объем V ₁, смешиваются с n ₂ молями другого газа, занимающего объем V ₂, то общий объем будет равен V ₁ + V ₂, причем газы расширяются независимо друг от друга и общее изменение энтропии равно сумме изменений энтропии каждого газа:

, (4.14)

где x_i - мольная доля i -го газа в полученной газовой смеси. Изменение энтропии (4.14) всегда положительно, т.к. все ln x_i < 0, поэтому идеальные газы всегда смешиваются необратимо.

Если при тех же условиях смешиваются две порции одного и того же газа, то уравнение (4.14) уже неприменимо. Никаких изменений в системе при смешивании не происходит, и S = 0. Тем не менее, формула (4.14) не содержит никаких индивидуальных параметров газов, поэтому, казалось бы, должна быть применима и к смешению одинаковых газов. Это противоречие называют парадоксом Гиббса.

Не нашли, что искали? Воспользуйтесь поиском: