
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Термодинамические потенциалы. Соотношения Максвелла
Термодинамическими потенциалами, или характеристическими функциями, называют термодинамические функции, которые содержат в себе всю термодинамическую информацию о системе. Наибольшее значение имеют четыре основных термодинамических потенциала:
1) внутренняя энергия U (S, V),
2) энтальпия H (S, p) = U + pV,
3) энергия Гельмгольца F (T, V) = U - TS,
4) энергия Гиббса G (T, p) = H - TS = F + pV.
В скобках указаны термодинамические параметры, которые получили название естественных переменных для термодинамических потенциалов. Все эти потенциалы имеют размерность энергии и все они не имеют абсолютного значения, поскольку определены с точностью до постоянной, которая равна внутренней энергии при абсолютном нуле.
Зависимость термодинамических потенциалов от их естественных переменных описывается основным уравнением термодинамики, которое объединяет первое и второе начала. Это уравнение можно записать в четырех эквивалентных формах:
dU = TdS - pdV (5.1)
dH = TdS + Vdp (5.2)
dF = - pdV - SdT (5.3)
dG = Vdp - SdT (5.4)
Эти уравнения записаны в упрощенном виде - только для закрытых систем, в которых совершается только механическая работа.
Зная любой из четырех потенциалов как функцию естественных переменных, можно с помощью основного уравнения термодинамики найти все другие термодинамические функции и параметры системы (см. пример 5-1).
Другой важный смысл термодинамических потенциалов состоит в том, что они позволяют предсказывать направление термодинамических процессов. Так, например, если процесс происходит при постоянных температуре и давлении, то неравенство, выражающее второй закон термодинамики:
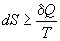
эквивалентно неравенству dG p,T  0 (мы учли, что при постоянном давлении
0 (мы учли, что при постоянном давлении  Qp = dH), где знак равенства относится к обратимым процессам, а неравенства - к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.
Qp = dH), где знак равенства относится к обратимым процессам, а неравенства - к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.
Аналогично, любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии:
| Потенциал | Естественные переменные | Условие само-произвольности | Условия равновесия |
| U | S = const, V = const | dU < 0 | dU = 0, d 2 U > 0 |
| H | S = const, p = const | dH < 0 | dH = 0, d 2 H > 0 |
| F | T = const, V = const | dF < 0 | dF = 0, d 2 F > 0 |
| G | T = const, p = const | dG < 0 | dG = 0, d 2 G > 0 |
Наибольшее значение в конкретных термодинамических расчетах имеют два последние потенциала - энергия Гельмгольца F и энергия Гиббса G, т.к. их естественные переменные наиболее удобны для химии. Другое (устаревшее) название этих функций - изохорно-изотермический и изобарно-изотермический потенциалы. Они имеют дополнительный физико-химический смысл. Уменьшение энергии Гельмгольца в каком-либо процессе при T = const, V = const равно максимальной механической работе, которую может совершить система в этом процессе:
F 1 - F 2 = A max (= A обр).
Таким образом, энергия F равна той части внутренней энергии (U = F + TS), которая может превратиться в работу.
Аналогично, уменьшение энергии Гиббса в каком-либо процессе при T = const, p = const равно максимальной полезной (т.е., немеханической) работе, которую может совершить система в этом процессе:
G 1 - G 2 = A пол.
Зависимость энергии Гельмгольца (Гиббса) от объема (давления) вытекает из основного уравнения термодинамики (5.3), (5.4):
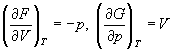 . (5.5)
. (5.5)
Зависимость этих функций от температуры можно описать с помощью основного уравнения термодинамики:
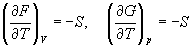 (5.6)
(5.6)
или с помощью уравнения Гиббса-Гельмгольца:
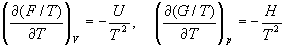 (5.7)
(5.7)
Расчет изменения функций F и G в химических реакциях можно проводить разными способами. Рассмотрим два из них на примере энергии Гиббса.
1) По определению, G = H - TS. Если продукты реакции и исходные вещества находятся при одинаковой температуре, то стандартное изменение энергии Гиббса в химической реакции равно:
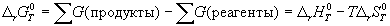 , (5.8)
, (5.8)
где тепловой эффект можно рассчитать с помощью стандартных энтальпий образования, а стандартное изменение энтропии - по абсолютным энтропиям участников реакции.
2) Аналогично тепловому эффекту реакции, изменение энергии Гиббса можно рассчитать, используя энергии Гиббса образования веществ:
 . (5.9)
. (5.9)
В термодинамических таблицах обычно приводят абсолютные энтропии и значения термодинамических функций образования соединений из простых веществ при температуре 298 К и давлении 1 бар (стандартное состояние). Для расчета  rG и
rG и  rF при других условиях используют соотношения (5.5) - (5.7).
rF при других условиях используют соотношения (5.5) - (5.7).
Все термодинамические потенциалы являются функциями состояния. Это свойство позволяет найти некоторые полезные соотношения между частными производными, которые называют соотношениями Максвелла.
Рассмотрим выражение (5.1) для внутренней энергии. Т.к. dU - полный дифференциал, частные производные внутренней энергии по естественным переменным равны:
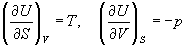
Если продифференцировать первое тождество по объему, а второе - по энтропии, то получатся перекрестные вторые частные производные внутренней энергии, которые равны друг другу:
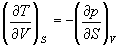 (5.10)
(5.10)
Три другие соотношения получаются при перекрестном дифференцировании уравнений (5.2) - (5.4).
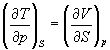 (5.11)
(5.11)
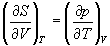 (5.12)
(5.12)
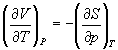 (5.13)
(5.13)
ПРИМЕРЫ
Пример 5-1. Внутренняя энергия некоторой системы известна как функция энтропии и объема, U (S, V). Найдите температуру и теплоемкость этой системы.
Решение. Из основного уравнения термодинамики (5.1) следует, что температура - это частная производная внутренней энергии по энтропии:
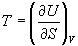 .
.
Изохорная теплоемкость определяет скорость изменения энтропии с температурой:
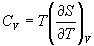 .
.
Воспользовавшись свойствами частных производных, можно выразить производную энтропии по температуре через вторую производную внутренней энергии:
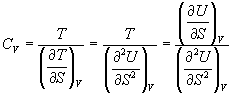 .
.
Пример 5-2. Используя основное уравнение термодинамики, найдите зависимость энтальпии от давления при постоянной температуре: а) для произвольной системы; б) для идеального газа.
Решение. а) Если основное уравнение в форме (5.2) поделить на dp при постоянной температуре, получим:
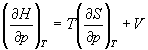 .
.
Производную энтропии по давлению можно выразить с помощью соотношения Максвелла для энергии Гиббса (5.13):
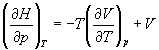 .
.
б) Для идеального газа V (T) = nRT / p. Подставляя эту функцию в последнее тождество, получим:
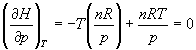 .
.
Энтальпия идеального газа не зависит от давления.
Пример 5-3. Выразите производные 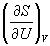 и
и 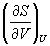 через другие термодинамические параметры.
через другие термодинамические параметры.
Решение. Основное уравнение термодинамики (5.1) можно переписать в виде:
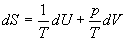 ,
,
представив энтропию как функцию внутренней энергии и объема. Коэффициенты при dU и dV равны соответствующим частным производным:
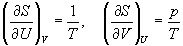 .
.
Пример 5-4. Два моля гелия (идеальный газ, мольная теплоемкость Cp = 5/2 R) нагревают от 100 оС до 200 оС при p = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия, 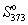 = 131.7 Дж/(моль. К). Можно ли считать этот процесс самопроизвольным?
= 131.7 Дж/(моль. К). Можно ли считать этот процесс самопроизвольным?
Решение. Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре (5.6):
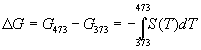 .
.
Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:
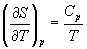 .
.
Интегрирование этого выражения от 373 К до T дает:
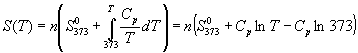 .
.
Подставляя это выражение в интеграл от энтропии, находим:
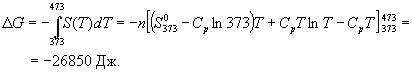
Процесс нагревания не обязан быть самопроизвольным, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при T = const и p = const.
Ответ.  G = -26850 Дж.
G = -26850 Дж.
Пример 5-5. Рассчитайте изменение энергии Гиббса в реакции
CO + ЅO2 = CO2
при температуре 500 K и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.
Решение. Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
| Вещество | Энтальпия образования 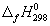 , кДж/моль , кДж/моль
| Энтропия 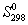 , Дж/(моль. К) , Дж/(моль. К)
| Теплоемкость 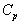 , Дж/(моль. К) , Дж/(моль. К)
|
| CO | -110.5 | 197.6 | 29.14 |
| O2 | 205.0 | 29.40 | |
| CO2 | -393.5 | 213.7 | 34.57 |
| Реакция |  , кДж/моль , кДж/моль
| 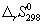 , Дж/(моль. К) , Дж/(моль. К)
|  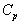 , Дж/(моль. К) , Дж/(моль. К)
|
| CO + ЅO2 = = CO2 | -283.0 | -86.4 | -9.27 |
Примем, что  Cp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
Cp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
 f = f (CO2) - f (CO) - Ѕ f (O2).
f = f (CO2) - f (CO) - Ѕ f (O2).
Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме (3.8):
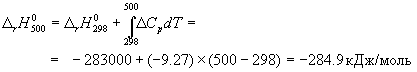
Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле (4.9):

Стандартное изменение энергии Гиббса при 500 К:
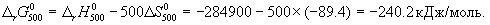
Для расчета изменения энергии Гиббса при парциальных давлениях 3 атм необходимо проинтегрировать формулу (5.5) и использовать условие идеальности газов ( V =
V =  n RT / p,
n RT / p,  n - изменение числа молей газов в реакции):
n - изменение числа молей газов в реакции):
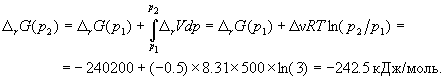
Эта реакция может протекать самопроизвольно при данных условиях.
Ответ.  G = -242.5 кДж/моль.
G = -242.5 кДж/моль.
ЗАДАЧИ
5-1. Выразите внутреннюю энергию как функцию переменных G, T, p.
5-2. Используя основное уравнение термодинамики, найдите зависимость внутренней энергии от объема при постоянной температуре: а) для произвольной системы; б) для идеального газа.
5-3. Известно, что внутренняя энергия некоторого вещества не зависит от его объема. Как зависит давление вещества от температуры? Ответ обоснуйте.
5-4. Выразите производные 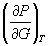 и
и 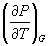 через другие термодинамические параметры и функции.
через другие термодинамические параметры и функции.
5-5. Напишите выражение для бесконечно малого изменения энтропии как функции внутренней энергии и объема. Найдите частные производные энтропии по этим переменным и составьте соответствующее уравнение Максвелла.
5-6. Для некоторого вещества известно уравнение состояния p (V, T). Как изменяется теплоемкость C v с изменением объема? Решите задачу: а) в общем виде; б) для какого-либо конкретного уравнения состояния (кроме идеального газа).
5-7. Докажите тождество: 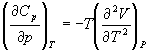 .
.
5-8. Энергия Гельмгольца одного моля некоторого вещества записывается следующим образом:
F = a + T (b - c - b ln T - d ln V),
где a, b, c, d - константы. Найдите давление, энтропию и теплоемкость C V этого тела. Дайте физическую интерпретацию константам a, b, d.
5-9. Нарисуйте график зависимости энергии Гиббса индивидуального вещества от температуры в интервале от 0 до T > T кип.
5-10. Для некоторой системы известна энергия Гиббса:
G (T, p) = aT (1-ln T) + RT ln p - TS 0 + U 0,
где a, R, S 0, U 0 - постоянные. Найдите уравнение состояния p (V, T) и зависимость U (V, T) для этой системы.
5-11. Зависимость мольной энергии Гельмгольца некоторой системы от температуры и объема имеет вид:
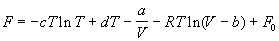 ,
,
где a, b, c, d - константы. Выведите уравнение состояния p (V, T) для этой системы. Найдите зависимость внутренней энергии от объема и температуры U (V, T). Каков физический смысл постоянных a, b, c?
5-12. Найдите зависимость мольной внутренней энергии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля)
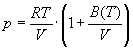 ,
,
где B (T) - известная функция температуры.
5-13. Для некоторого вещества зависимость теплоемкости от температуры имеет вид: C V = aT 3 при температуре 0 - 10 К. Найдите зависимость энергии Гельмгольца, энтропии и внутренней энергии от температуры в этом диапазоне.
5-14. Для некоторого вещества зависимость внутренней энергии от температуры имеет вид: U = aT 4 + U 0 при температуре 0 - 10 К. Найдите зависимость энергии Гельмгольца, энтропии и теплоемкости C V от температуры в этом диапазоне.
5-15. Выведите соотношение между теплоемкостями:
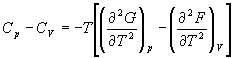 .
.
5-16. Исходя из тождества 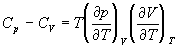 , докажите тождество:
, докажите тождество:
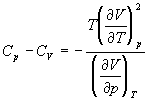 .
.
5-17. Один моль газа Ван-дер-Ваальса изотермически расширяется от объема V 1 до объема V 2 при температуре T. Найдите  U,
U,  H,
H,  S,
S,  F и
F и  G для этого процесса.
G для этого процесса.
5-18. Вычислите изменение H, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0.5 м3 до 1.35 м3 0.7 молей азота (C V = 5/2 R). Энтропия газа в исходном состоянии равна 150 Дж/(моль. К), газ можно считать идеальным.
5-19. Вычислите изменение энергии Гиббса при сжатии от 1 атм до 3 атм при 298 К: а) одного моля жидкой воды; б) одного моля водяного пара (идеальный газ).
5-20. Изменение энергии Гиббса в результате испарения воды при 95 оС и 1 атм равно 546 Дж/моль. Рассчитайте энтропию паров воды при 100 оС, если энтропия жидкой воды равна 87.0 Дж/(моль. К). При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 95 оС?
5-21*. Давление над одним молем твердой меди при температуре 25оС увеличили от 1 до 1000 атм. Найти  U,
U,  H,
H,  S,
S,  F. Медь считать несжимаемой, плотность 8.96 г/см3, изобарический коэффициент теплового расширения
F. Медь считать несжимаемой, плотность 8.96 г/см3, изобарический коэффициент теплового расширения 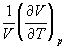 = 5.01. 10-5 К-1.
= 5.01. 10-5 К-1.
5-22. Вычислите стандартную энергию Гиббса образования (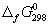 ) жидкой и газообразной воды, если известны следующие данные:
) жидкой и газообразной воды, если известны следующие данные: 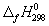 (H2O(г)) = -241.8 кДж/моль,
(H2O(г)) = -241.8 кДж/моль, 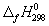 (H2O(ж)) = -285.6 кДж/моль,
(H2O(ж)) = -285.6 кДж/моль, 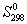 (H2) = 130.6 Дж/(моль. К),
(H2) = 130.6 Дж/(моль. К), 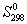 (O2) = 205.0 Дж/(моль. К),
(O2) = 205.0 Дж/(моль. К), 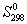 (H2O(г)) = 188.5 Дж/(моль. К),
(H2O(г)) = 188.5 Дж/(моль. К), 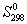 (H2O(ж)) = 69.8 Дж/(моль. К).
(H2O(ж)) = 69.8 Дж/(моль. К).
5-23. Рассчитайте  G o при 25 оС для химической реакции:
G o при 25 оС для химической реакции:
4HCl(г) + O2(г) = 2Cl2(г) + 2H2O(ж).
Стандартные значения энтальпии образования и абсолютной энтропии при 25 оС равны:  fH o(HСl) = -22.1 ккал/моль,
fH o(HСl) = -22.1 ккал/моль,  fH o(H2O(ж)) = -68.3 ккал/моль; S o(HCl) = 44.6 кал/(моль. K), S o(O2) = 49.0 кал/(моль. K), S o(Сl2) = 53.3 кал/(моль. K), S o(H2O(ж)) = 16.7 кал/(моль. K).
fH o(H2O(ж)) = -68.3 ккал/моль; S o(HCl) = 44.6 кал/(моль. K), S o(O2) = 49.0 кал/(моль. K), S o(Сl2) = 53.3 кал/(моль. K), S o(H2O(ж)) = 16.7 кал/(моль. K).
5-24. Рассчитайте  G o при 25 оС для химической реакции:
G o при 25 оС для химической реакции:
CO2(г) + 4H2(г) = CH4(г) + 2H2O(ж).
Стандартные значения энтальпии образования и абсолютной энтропии при 25 оС равны:  fH o(СO2) = -94.1 ккал/моль,
fH o(СO2) = -94.1 ккал/моль,  fH o(СH4) = -17.9 ккал/моль,
fH o(СH4) = -17.9 ккал/моль,  fH o(H2O(ж)) = -68.3 ккал/моль; S o(СO2) = 51.1 кал/(моль. K), S o(H2) = 31.2 кал/(моль. K), S o(СH4) = 44.5 кал/(моль. K), S o(H2O(ж)) = 16.7 кал/(моль. K).
fH o(H2O(ж)) = -68.3 ккал/моль; S o(СO2) = 51.1 кал/(моль. K), S o(H2) = 31.2 кал/(моль. K), S o(СH4) = 44.5 кал/(моль. K), S o(H2O(ж)) = 16.7 кал/(моль. K).
5-25. Рассчитайте стандартные энергии Гиббса и Гельмгольца  G o и
G o и  F o при 300 оС для химической реакции:
F o при 300 оС для химической реакции:
CO(г) + 3H2(г) = CH4(г) + H2O(г).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-26. Найдите энергию Гиббса образования NH3 при температурах 298 и 400 K, если известны следующие данные: 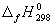 (NH3) = -46.2 кДж/моль,
(NH3) = -46.2 кДж/моль,
| Вещество | N2 | H2 | NH3 |
| Cp,298, Дж/(моль. К) | 29.1 | 28.8 | 35.7 |
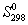 , Дж/(моль. К) , Дж/(моль. К)
| 191.5 | 130.6 | 192.5 |
Считать, что теплоемкости в указанном интервале температур постоянны.
5-27. Рассчитайте стандартные энергии Гиббса и Гельмгольца  G o и
G o и  F o при 60 оС для химической реакции:
F o при 60 оС для химической реакции:
CH3COOH(ж) + 2H2(г) = C2H5OH(ж) + H2O(ж).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
5-28. Рассчитайте стандартные энергии Гиббса и Гельмгольца  G o и
G o и  F o при 700 оС для химической реакции:
F o при 700 оС для химической реакции:
CaCO3(тв) = CaO(тв) + CO2(г).
Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.
Не нашли, что искали? Воспользуйтесь поиском: