
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Фазовое равновесие в однокомпонентных системах
Условием равновесия между двумя фазами является равенство давления, температуры и химических потенциалов (мольных энергий Гиббса) в обеих фазах. Если температура изменяется при постоянном давлении или давление изменяется при постоянной температуре, то равновесие нарушается и одна из фаз исчезает. Изменение химических потенциалов фаз при этом можно рассчитать по уравнениям:
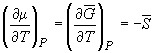 , (6.1)
, (6.1)
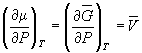 , (6.2)
, (6.2)
где 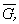
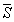 и
и 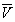 – мольные энергия Гиббса, энтропия и объем.
– мольные энергия Гиббса, энтропия и объем.
Условие сосуществования двух фаз при одновременном изменении давления P и температуры T описывается уравнением Клапейрона:
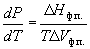 , (6.3)
, (6.3)
где  H ф.п. – мольная энтальпия равновесного фазового перехода (плавление, испарение, возгонка, переход между модификациями),
H ф.п. – мольная энтальпия равновесного фазового перехода (плавление, испарение, возгонка, переход между модификациями),  V ф.п. – разность мольных объемов фаз, находящихся в равновесии.
V ф.п. – разность мольных объемов фаз, находящихся в равновесии.
В случаях испарения и возгонки уравнение (6.3) можно упростить, считая, что мольным объемом конденсированной фазы (жидкости или твердого тела) V к.ф.по сравнению с мольным объемом пара V пар можно пренебречь и что пар подчиняется уравнению состояния идеального газа. Подставляя (V пар– V к.ф.) 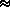 V пари V пар= RT / P, получаем уравнение Клаузиуса-Клапейрона:
V пари V пар= RT / P, получаем уравнение Клаузиуса-Клапейрона:
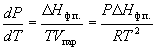 (6.4)
(6.4)
или после преобразования
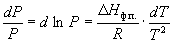 . (6.5)
. (6.5)
Интегрирование в предположении, что  H ф.п. не зависит от температуры (что справедливо в узких интервалах температур), дает
H ф.п. не зависит от температуры (что справедливо в узких интервалах температур), дает
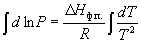 (6.6)
(6.6)
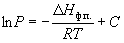 (6.7)
(6.7)
где C – константа интегрирования. Следовательно, зависимость ln P от 1 /Т должна быть линейной, а наклон прямой равен –  H ф.п./ R.
H ф.п./ R.
Интегрирование в пределах P 1, P 2, и T 1, T 2 дает:
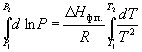 (6.8)
(6.8)
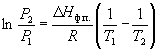 (6.9)
(6.9)
По этому уравнению можно рассчитать энтальпию испарения или возгонки, исходя из значений давления пара при двух разных температурах.
Мольные энтальпии возгонки, плавления и испарения при данной температуре связаны соотношением
 возг H =
возг H =  пл H +
пл H +  исп H (6.10)
исп H (6.10)
Энтальпию испарения жидкости можно приближенно оценить по правилу Трутона, согласно которому мольная энтропия испарения в нормальной точке кипения (при 1 атм) приблизительно постоянна:
 исп S =
исп S = 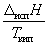
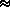 88 Дж. моль–1. К–1 (6.11)
88 Дж. моль–1. К–1 (6.11)
Правило хорошо выполняется для неполярных жидкостей.
Зависимость энтальпии фазового перехода от температуры можно рассчитать по закону Кирхгофа:
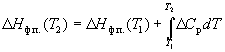 (6.12)
(6.12)
или
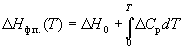 (6.13)
(6.13)
где  C p – разность теплоемкостей фаз, находящихся в равновесии,
C p – разность теплоемкостей фаз, находящихся в равновесии,  H 0 – константа интегрирования, определяемая из известных значений
H 0 – константа интегрирования, определяемая из известных значений  H ф.п. и
H ф.п. и  C p. Для небольших интервалов температуры можно считать, что
C p. Для небольших интервалов температуры можно считать, что  C p = const. В этом случае из уравнения (6.13) получаем:
C p = const. В этом случае из уравнения (6.13) получаем:
 H ф.п. (T) =
H ф.п. (T) =  H 0 + T
H 0 + T  Cp. (6.14)
Cp. (6.14)
Подставляя уравнение (6.14) в уравнение (6.7), получаем:
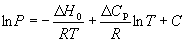 , (6.15)
, (6.15)
в котором С определяют из известных значений P,  H 0 и
H 0 и  C p.
C p.
ПРИМЕРЫ
Пример 6-1. Рассчитать изменение давления, необходимое для изменения температуры плавления льда на 1o C. При 0o C энтальпия плавления льда равна 333.5 Дж. г–1, удельные объемы жидкой воды и льда равны V ж. = 1.0002 см3. г–1 и V тв. = 1.0908 см3. г–1.
Решение. Изменение объема при плавлении льда равно
V ж. – V тв. = 1.0002 – 1.0908 = –0.0906 см3. г–1 = –9.06  10–8 м3. г–1.
10–8 м3. г–1.
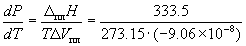 = –1.348
= –1.348  107 (Па. К–1) = –133 атм. К–1.
107 (Па. К–1) = –133 атм. К–1.
Таким образом, при повышении давления на 133 атм температура плавления льда понижается на 1 градус. Знак "минус" показывает, что при повышении давления температура плавления понижается.
Ответ.  P = 133 атм.
P = 133 атм.
Пример 6-2. Рассчитать давление пара жидкого брома при 25o C.  fGo газообразного брома равна 3.110 кДж. моль–1.
fGo газообразного брома равна 3.110 кДж. моль–1.
Решение.  исп Go брома равно
исп Go брома равно  fGo [Br2 (г)] = 3110 Дж. моль–1.
fGo [Br2 (г)] = 3110 Дж. моль–1.
 исп Go =
исп Go = 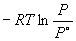 , откуда P = 0.2852 атм.
, откуда P = 0.2852 атм.
Ответ. P = 0.2852 атм.
Пример 6-3. Рассчитать давление, при котором графит и алмаз находятся в равновесии при 25o C.  fGo алмаза равна 2.900 кДж. моль–1. Считать плотности графита и алмаза равными 2.25 и 3.51 г. см–3 соответственно и не зависящими от давления.
fGo алмаза равна 2.900 кДж. моль–1. Считать плотности графита и алмаза равными 2.25 и 3.51 г. см–3 соответственно и не зависящими от давления.
Решение. Изменение объема при переходе от графита к алмазу равно
 V = 12.
V = 12. 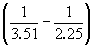
 10–6 = –1.91
10–6 = –1.91  10–6 м3. моль–1
10–6 м3. моль–1
При начальном давлении P 1 разность мольных энергий Гиббса  G 1 = 2900 Дж. моль–1, а при конечном давлении P 2 разность
G 1 = 2900 Дж. моль–1, а при конечном давлении P 2 разность  G 2 =0.
G 2 =0.
Поскольку 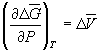 , то
, то 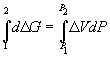 =
=  G 2 –
G 2 –  G 1 =
G 1 =  V (P 2 – P 1).
V (P 2 – P 1).
Отсюда P 2 = 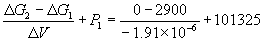 = 1.52
= 1.52  109 Па = 1.5
109 Па = 1.5  104 атм.
104 атм.
Ответ. P = 1.5  104 атм.
104 атм.
Пример 6-4. Температура кипения бензола при давлении 1 атм равна 80.1o C. Оценить давление пара бензола при 25o C.
Решение. Давление пара бензола при T 1 = 353.3 K равно P 1 = 1 атм. По правилу Трутона  исп H = 88. 353.3 = 31.1 кДж. моль–1. Подставим эти данные в уравнение (6.9). Получим:
исп H = 88. 353.3 = 31.1 кДж. моль–1. Подставим эти данные в уравнение (6.9). Получим:
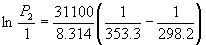 , откуда P 2 = 0.141 атм.
, откуда P 2 = 0.141 атм.
Ответ. P = 0.141 атм.
ЗАДАЧИ
1. Рассчитать давление, при котором две формы CaCO3 – кальцит и арагонит – находятся в равновесии при 25o C.  fGo кальцита и арагонита при 25o C равны –1128.79 и –1127.75 кДж. моль–1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г. см–3 соответственно и не зависят от давления.
fGo кальцита и арагонита при 25o C равны –1128.79 и –1127.75 кДж. моль–1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г. см–3 соответственно и не зависят от давления.
2. Рассчитать температуру, при которой две формы CaCO3 – кальцит и арагонит – находятся в равновесии при давлении 1 атм. При 25o C  fGo кальцита и арагонита равны –1128.79 и –1127.75 кДж. моль–1 соответственно,
fGo кальцита и арагонита равны –1128.79 и –1127.75 кДж. моль–1 соответственно,  fHo равны–1206.92 и –1207.13 кДж. моль–1 соответственно. Считать, что
fHo равны–1206.92 и –1207.13 кДж. моль–1 соответственно. Считать, что  C P = 0.
C P = 0.
3.  fGo жидкой и газообразной воды при 25o C равны –237.129 и –228.572 кДж. моль–1 соответственно. Рассчитать давление пара воды при 25o C.
fGo жидкой и газообразной воды при 25o C равны –237.129 и –228.572 кДж. моль–1 соответственно. Рассчитать давление пара воды при 25o C.
4. Плотности жидкого и твердого олова при температуре плавления (231.9o C) равны 6.980 г. см–3 и 7.184 г. см–3 соответственно. Энтальпия плавления олова равна 1.690 ккал. моль–1. Определить температуру плавления олова под давлением 500 атм. Молярная масса олова равна 118.7 г. моль–1.
5. При замерзании бензола (5.5oC) его плотность изменяется от 0.879 г. см–3 до 0.891 г. см–3. Энтальпия плавления равна 10.59 кДж. моль–1. Определить температуру плавления бензола при давлении 1000 атм.
6. Плотности жидкой и твердой ртути при температуре плавления
(–38.87oC) равны 13.690 и 14.193 г. см–3 соответственно. Энтальпия плавления ртути равна 2.33 кал. г–1. Определить температуру плавления ртути при давлении 3000 атм.
7. Температура кипения жидкого метанола равна 34.7 o C при давлении 200 мм рт. ст. и 49.9 o C при давлении 400 мм рт. ст. Найти температуру кипения метанола при нормальном давлении.
8. Давление пара диэтилового эфира при 10o C равно 286.8 мм рт. ст., а при 20o C – 432.8 мм рт. ст. Определить мольную энтальпию испарения и нормальную температуру кипения эфира.
9. Давление пара дихлорметана при 24.1oC равно 400 Торр, а его энтальпия испарения равна 28.7 кДж. моль–1. Рассчитать температуру, при которой давление пара будет равно 500 Торр.
10. Давление пара твердого CO2 равно 133 Па при –134.3 o C и 2660 Па при –114.4 o C. Рассчитать энтальпию возгонки.
11. Давление пара (Торр) жидкости в интервале температур 200 – 260 K описывается уравнением:
ln p = 16.255 – 2501.8 / T.
Рассчитать энтальпию испарения и нормальную точку кипения жидкости.
12. Давление пара (Торр) жидкого бензола C6H6 между 10oC и 80oC описывается уравнением:
lg p = 7.960 – 1780 / T.
Рассчитать энтальпию испарения и нормальную точку кипения бензола.
13. Давление пара жидкого нафталина C10H8 равно 10 Торр при 85.8oC и 40 Торр при 119.3oC. Определить энтальпию испарения, нормальную точку кипения и энтропию испарения в нормальной точке кипения.
14. Нормальная точка кипения гексана равна 69.0єC. Оценить а) мольную энтальпию испарения и б) давление пара гексана при 25єC и 60єC.
15. При 0oC энтальпии испарения и плавления воды равны 595 и 79.7 кал. г–1 соответственно. Давление пара воды при 0oC равно 4.58 мм рт. ст. Рассчитать давление пара льда при –15oC, считая, что изменение энтальпии не зависит от температуры.
16. Рассчитать температуру кипения воды на вершине Эвереста (высота 8850 м). Энтальпию испарения воды считать равной 40.67 кДж. моль–1. Для расчета атмосферного давления на вершине воспользоваться барометрической формулой.
17. Уксусная кислота имеет следующие давления насыщенного пара:
| T, K | |||
| P, мм. рт. ст. |
18. Определить молярную массу уксусной кислоты в паре, если известно, что "исп H = 24.35 кДж. моль–1.
19. Давление пара (в мм рт. ст.) твердого и жидкого SO2 выражается уравнениями
lg P (тв) = 10.5916 – 1871.2/ T
lg P (ж) = 8.3186 – 1425.7/ T
Рассчитать температуру, давление и  пл H SO2 в тройной точке.
пл H SO2 в тройной точке.
20. Давление пара (в мм рт. ст.) над твердым и жидким UF6 выражается уравнениями
lg P (тв) = 10.648 – 2559.5/ T
lg P (ж) = 7.540 – 1511.3/ T
Рассчитать температуру, давление и  пл H UF6 в тройной точке.
пл H UF6 в тройной точке.
21. Давление пара над твердым Cl2 равно 352 Па при –112oC и 35 Па при –126.5oC, а давление пара над жидким Cl2 равно 1590 Па при –100oC и 7830 Па при –80oC. Определить координаты тройной точки и  пл H Cl2.
пл H Cl2.
22. Давление пара над твердым C6H6 равно 299 Па при –30oC и 3270 Па при 0oC, а давление пара над жидким C6H6 равно 6170 Па при 10oC и 15800 Па при 30oC. Определить координаты тройной точки и  пл H C6H6.
пл H C6H6.
23. Давление пара над твердым SnBr4 равно 0.116 мм рт. ст. при 9.8 oC и 0.321 мм рт. ст. при 21.0 oC, а давление пара над жидким SnBr4 равно 0.764 мм рт. ст. при 30.7 oC и 1.493 мм рт. ст. при 41.4 oC. Определить координаты тройной точки и  пл H SnBr4.
пл H SnBr4.
24. Давление пара 2,2-диметилбутанола-1 (мм рт. ст.) выражается уравнением:
lg p = –4849.3/ T – 14.701 lg T + 53.1187.
Рассчитать а) нормальную точку кипения, б) энтальпию испарения в нормальной точке кипения, в) энтальпию испарения при 25o C.
25. Давление пара ртути (мм рт. ст.) в интервале 298 – 630 К выражается уравнением:
lg p = –3308/ T – 0.8 lg T + 10.373.
Рассчитать а) нормальную точку кипения ртути и б) энтальпию испарения ртути в нормальной точке кипения.
26. Рассчитать давление пара воды при 200o C, принимая, что а)  H исп = 40.67 кДж. моль–1 и не зависит от температуры; б)
H исп = 40.67 кДж. моль–1 и не зависит от температуры; б)  C p = –42 Дж. моль–1. К–1.
C p = –42 Дж. моль–1. К–1.
Не нашли, что искали? Воспользуйтесь поиском: