Примеры решения задач на тему. «Молекулярно-кинетическая теория идеального газа»

«Молекулярно-кинетическая теория идеального газа»

Задача 1. Баллон содержит 80 г кислорода и 300 г аргона. Давление смеси 10 атм, температура 15⁰С. Принимая данные газы за идеальные, определить емкость баллона.

Дано: m₁ = 80 г = 8^.10^-2кг;

Аr m₂ = 300 г = 3^.10^-1кг;

t = 15⁰C; Т = 288К.

P = 10 атм = 1,01^.10⁶ Па.

_____________________

V -?

Решение.

По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. Парциальным давлением газа называется давление, которое производил бы газ, если бы только он один находился в сосуде, занятом смесью.

По уравнению Менделеева-Клапейрона парциальные давления кислорода P₁ и аргона P₂ выражаются формулами

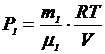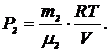и (1)

По закону Дальтона для смеси газов

P = P₁ + P₂, (2)

или

(3)

где - молярная газовая постоянная

Из (3) выражаем объем баллона:

(4)

Проверим размерность расчетной формулы:

.

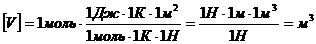Подставим числовые значения в формулу (4) и произведем вычисления:

Ответ: объем баллона равен 24 л.

Задача 2. Найти кинетическую энергию вращательного движения одной молекулы кислорода при температуре 13⁰С, а также кинетическую энергию вращательного движения всех молекул, содержащихся в 4 г кислорода.

Дано:

;

_____________

e_вр -? W_вр -?

Решение.

Известно, что на каждую степень свободы молекулы газа приходится одинаковая энергия, выражаемая формулой

(1)

где k - постоянная Больцмана, T - абсолютная температура газа.

Так как вращательному движению двухатомной молекулы (молекула кислорода - двухатомная) приписываются две степени свободы, то энергия вращательного движения молекулы кислорода выразится формулой

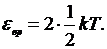(2)

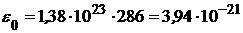(Дж).

Кинетическая энергия вращательного движения всех молекул газа:

, (3)

где N - число всех молекул газа.

Число молекул N можно получить по формуле

(4)

где N_A - число Авогадро, n - количество вещества в молях:

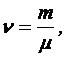
где m - масса газа, m - масса одного моля газа, следовательно,

(5)

Подставив это выражение N в формулу (3), получим

(6)

Подставим численные значения физических величин в формулу (6) и произведем вычисления, получим:

Ответ: кинетическая энергия вращательного движения одной молекулы кислорода при температуре 13⁰С равна Дж, кинетическая энергия вращательного движения всех молекул равна 296 Дж.

Задача 3. В современной вакуумной камере достигается вакуум порядка 0,1 нПа. Какова средняя длина свободного пробега молекул азота в камере при температуре . Чему равно среднее число столкновений каждой молекулы с остальными в единицу времени?

(Массу молекулы азота считать равной 5^.10^{-20 кг).}

Дано:

N₂

P =0,1 нПа=10^-10Па;

; Т =300К;

m₁ = 5^.10^{-20 кг.}

_________________

-? <z> -?

Решение.

Средняя длина свободного пробега молекул определяется из соотношения:

, (1)

где < v > - средняя арифметическая скорость молекул,

< z > - среднее число столкновений каждой молекулы с остальными в единицу времени,

n - концентрация молекул газа, 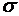- эффективный диаметр молекулы.

Концентрация молекул газа связана с его давлением соотношением:

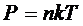, (2)

где к – постоянная Больцмана, Т – термодинамическая температура.

Таким образом,

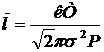. (3)

Эффективный диаметр молекулы 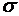=3 10^-10м,

Постоянная Больцмана к =1,38 10^-23 Дж/К,

Произведем вычисления по формуле (3):

.

Из формулы (1) выразим среднее число столкновений <z> молекул в единицу времени:

, (4)

где средняя арифметическая скорость молекул

. (5)

Подставим выражение (5) в формулу (4), получим::

,

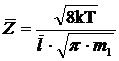где - постоянная Больцмана; Т- термодинамическая температура;

- средняя длина свободного пробега молекул; 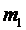- масса одной молекулы.

Произведем вычисления:

.

Ответ: средняя длина свободного пробега молекул равна ; среднее число столкновений, испытуемых одной молекулой в единицу времени, равно .

Задача 4. Азот находится по давлением при температуре 290 К. Определите коэффициент диффузии D и внутреннего трения . Эффективный диаметр молекул азота принять равным .

Дано: ;

;

__________________________

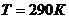Решение.

На основании представлений молекулярно-кинетической теории газов коэффициент внутреннего трения идеального газа (динамическая вязкость) и коэффициент диффузии определяются по формулам:

, (1)

; (2)

(3)

где - средняя длина свободного пробега молекул азота;

- коэффициент внутреннего трения;

- коэффициент диффузии;

n - концентрация молекул газа;

- средняя скорость молекул газа;

- масса одной молекулы;

эффективный диаметр молекул газа.

Концентрацию молекул газа по заданным значениям давления и температуры определим из основного уравнения молекулярно-кинетической теории газов:

. (4)

Выражая концентрацию из уравнения (4) и подставляя в формулу (1) получим

Проверка размерности расчетной формулы:

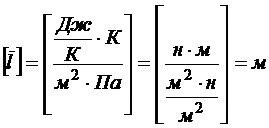
Средняя скорость молекул

, (5)

где – молярная газовая постоянная;

Т – термодинамическая температура;

- молярная масса азота.

Вычислим среднюю скорость молекул азота:

.

Проверка размерности расчетной формулы:

;

Для расчета коэффициента диффузии воспользуемся полученными результатами:

.

Для расчета коэффициента внутреннего трения подставим в формулу (3) концентрацию n и массу одной молекулы азота , учитывая, что

;

;

Имеем:

;

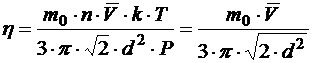Масса одной молекулы газа

,

где - молярная масса газа, постоянная Авогадро.

Произведем вычисления:

;

.

Проверка размерности расчетной формулы:

Ответ: коэффициент диффузии равен ,

коэффициент внутреннего трения равен .

Задача N 5. Каково давление воздуха в шахте на глубине 1 км, если считать, что температура по всей высоте постоянна и равна 22 С, а ускорение свободного падения не зависит от высоты. Давление воздуха у поверхности Земли принять равным .

Дано:

Решение.

Воспользуемся барометрической формулой:

, (1)

где и - давления воздуха на высоте и соответственно;

- молярная масса воздуха;

- ускорение свободного падения;

- молярная газовая постоянная;

- термодинамическая температура.

За начало отсчета высоты примем дно шахты, тогда ;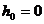

112291,9 .

Ответ: давление воздуха на дне шахты .

Основы термодинамики

Не нашли, что искали? Воспользуйтесь поиском: