Перпендикуляр и наклонная

Теорема. Если из одной точки вне плоскости проведены перпендикуляр и наклонные, то:

1) наклонные, имеющие равные проекции, равны;

2) из двух наклонных больше та, проекция которой больше;

3) равные наклонные имеют равные проекции;

4) из двух проекций больше та, которая соответствует большей наклонной.

Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной (рис. 12.3).

Теорема о площади ортогональной проекции многоугольника на плоскость. Площадь ортогональной проекции многоугольника на плоскость равна произведению площади многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

Рис. 12.3

Пример 1. Через данную точку провести прямую, параллельную данной плоскости.

Решение. Анализ. Предположим, что прямая построена (рис. 12.4). Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в плоскости (по признаку параллельности прямой и плоскости). Две параллельные прямые лежат в одной плоскости. Значит, построив плоскость, проходящую через данную точку и произвольную прямую в данной плоскости, можно будет построить параллельную прямую.

Рис. 12.4

Построение.

1. На плоскости a проводим прямую а.

2. Прямая а и точка А задают плоскость. Построим плоскость b.

3. В плоскости b через точку А проведем прямую b, параллельную прямой а.

4. Построена прямая b, параллельная плоскости a.

Доказательство. По признаку параллельности прямой и плоскости прямая b параллельна плоскости a, так как она параллельна прямой а, принадлежащей плоскости a.

Исследование. Задача имеет бесконечное множество решений, так как прямая а в плоскости a выбирается произвольно.

Пример 2. Определите, на каком расстоянии от плоскости находится точка А, если прямая АВ пересекает плоскость под углом 45º, расстояние от точки А до точки В, принадлежащей плоскости, равно см.

Решение. Сделаем рисунок (рис. 12.5):

Рис. 12.5

АС – перпендикуляр к плоскости a, АВ – наклонная, угол АВС – угол между прямой АВ и плоскостью a. Треугольник АВС – прямоугольный, так как АС – перпендикуляр. Искомое расстояние от точки А до плоскости – это катет АС прямоугольного треугольника. Зная угол 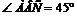и гипотенузу найдем катет АС:

В ответе получаем: АС = 3 см.

Пример 3. Определите, на каком расстоянии от плоскости равнобедренного треугольника находится точка, удаленная от каждой из вершин треугольника на 13 см, если основание и высота треугольника равны по 8 см.

Решение. Сделаем рисунок (рис. 12.6). Точка S удалена от точек А, В и С на одинаковое расстояние. Значит, наклонные SA, SB и SC равные, SO – общий перпендикуляр этих наклонных. По теореме о наклонных и проекциях АО = ВО = СО.

Точка О – центр окружности, описанной около треугольника АВС. Найдем ее радиус:

Рис. 12.6

где ВС – основание; AD – высота данного равнобедренного треугольника.

Находим стороны треугольника АВС из прямоугольного треугольника ABD по теореме Пифагора:

Теперь находим ОВ:

Рассмотрим треугольник SOB: SB = 13 см, ОВ = 5 см. Находим длину перпендикуляра SO по теореме Пифагора:

В ответе получаем: SO = 12 см.

Пример 4. Даны параллельные плоскости a и b. Через точку М, не принадлежащую ни одной из них, проведены прямые а и b, которые пересекают плоскость a в точках А ₁ и В ₁, а плоскость b – в точках А ₂ и В ₂. Найти А ₁ В ₁, если известно, что МА ₁ = 8 см, А ₁ А ₂ = 12 см, А ₂ В ₂ = 25 см.

Решение. Так как в условии не сказано, как расположена относительно обеих плоскостей точка М, то возможны два варианта: (рис. 12.7, а, б). Рассмотрим каждый из них. Две пересекающиеся прямые а и b задают плоскость. Эта плоскость пересекает две параллельные плоскости a и b по параллельным прямым А ₁ В ₁ и А ₂ В ₂ согласно теореме 5 о параллельных прямых и параллельных плоскостях.

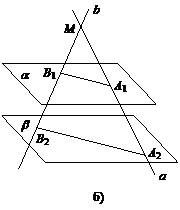Рис. 12.7

Треугольники МА ₁ В ₁ и МА ₂ В ₂ подобны (углы А ₂ МВ ₂ и А ₁ МВ ₁ – вертикальные, углы МА ₁ В ₁ и МА ₂ В ₂ – внутренние накрест лежащие при параллельных прямых А ₁ В ₁ и А ₂ В ₂ и секущей А ₁ А ₂). Из подобия треугольников следует пропорциональность сторон:

Отсюда

Вариант а):

Вариант б):

Получаем ответ: 10 см и 50 см.

Пример 5. Через точку А плоскости g проведена прямая АВ, образующая с плоскостью угол a. Через прямую АВ проведена плоскость r, образующая с плоскостью g угол b. Найти угол между проекцией прямой АВ на плоскость g и плоскостью r.

Решение. Сделаем рисунок (рис. 12.8). Из точки В опустим перпендикуляр на плоскость g. Линейный угол двугранного угла между плоскостями g и r – это угол Прямая AD перпендикулярна плоскости треугольника DBC, по признаку перпендикулярности прямой и плоскости, так как и По признаку перпендикулярности плоскостей плоскость r перпендикулярна плоскости треугольника DBC, так как она проходит через прямую AD. Искомый угол построим, опустив перпендикуляр из точки С на плоскость r, обозначим его Найдем синус этого угла прямоугольного треугольника САМ. Введем вспомогательный отрезок ВС = а. Из треугольника АВС: Из треугольника ВМС ( )найдем:

Тогда искомый угол

Рис. 12.8

Получаем ответ: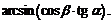

Задания

I уровень

1.1. Через точку проведите прямую, перпендикулярную двум заданным скрещивающимся прямым.

1.2. Определите, сколько различных плоскостей можно провести:

1) через три различные точки;

2) через четыре различные точки, никакие три из которых не лежат на одной плоскости.

1.3. Через вершины треугольника АВС, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А ₁, В ₁, С ₁. Докажите равенство треугольников АВС и А ₁ В ₁ С ₁.

1.4. Из вершины А прямоугольника ABCD восставлен перпендикуляр АМ к его плоскости.

1) докажите, что треугольники MBC и MDC – прямоугольные;

2) укажите среди отрезков MB, MC, MD и MA отрезок наибольшей и наименьшей длины.

1.5. Грани одного двугранного угла соответственно параллельны граням другого. Определите, какова зависимость между величинами этих двугранных углов.

1.6. Найдите величину двугранного угла, если расстояние от точки, взятой на одной грани, до ребра в 2 раза больше расстояния от точки до плоскости второй грани.

1.7. Из точки, отстоящей от плоскости на расстояние проведены две равные наклонные, образующие угол 60º. Проекции наклонных взаимно перпендикулярны. Найдите длины наклонных.

1.8. Из вершины В квадрата ABCD восставлен перпендикуляр ВЕ к плоскости квадрата. Угол наклона плоскости треугольника АСЕ к плоскости квадрата равен j, сторона квадрата равна а. Найдите площадь треугольника АСЕ.

II уровень

2.1. Через точку, которая не принадлежит ни одной из двух скрещивающихся прямых, проведите прямую, пересекающую обе данные прямые.

2.2. Параллельные прямые а, b и с не лежат в одной плоскости. Через точку А на прямой а проведены перпендикуляры к прямым b и с, пересекающие их соответственно в точках В и С. Докажите, что прямая ВС перпендикулярна прямым b и с.

2.3. Через вершину А прямоугольного треугольника АВС проведена плоскость, параллельная ВС. Катеты треугольника АС = 20 см, ВС = 15 см. Проекция одного из катетов на плоскость равна 12 см. Найдите проекцию гипотенузы.

2.4. В одной из граней двугранного угла, равного 30º, расположена точка М. Расстояние от нее до ребра угла равно 18 см. Найдите расстояние от проекции точки М на вторую грань до первой грани.

2.5. Концы отрезка АВ принадлежат граням двугранного угла, равного 90º. Расстояние от точек А и В до ребра равны соответственно АА ₁ = 3 см, ВВ ₁ = 6 см, расстояние между точками на ребре – Найдите длину отрезка АВ.

2.6. Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные, образующие с плоскостью углы 45º и 30º, а между собой угол 90º. Найдите расстояние между основаниями наклонных.

2.7. Стороны треугольника равны 15 см, 21 см и 24 см. Точка М удалена от плоскости треугольника на 73 см и находится на одинаковом расстоянии от его вершин. Найдите это расстояние.

2.8. Из центра О окружности, вписанной в треугольник АВС, к плоскости треугольника восставлен перпендикуляр ОМ. Найдите расстояние от точки М до сторон треугольника, если АВ = ВС = 10 см, АС = 12 см, ОМ = 4 см.

2.9. Расстояния от точки М до сторон и вершины прямого угла соответственно равны 4 см, 7 см и 8 см. Найдите расстояние от точки М до плоскости прямого угла.

2.10. Через основание АВ равнобедренного треугольника АВС проведена плоскость под углом b к плоскости треугольника. Вершина С удалена от плоскости на расстояние а. Найдите площадь треугольника АВС, если основание АВ равнобедренного треугольника равно его высоте.

III уровень

3.1. Макет прямоугольника ABCD со сторонами а и b перегнут по диагонали BD так, что плоскости треугольников BAD и BCD стали взаимно перпендикулярны. Найдите длину отрезка АС.

3.2. Две прямоугольные трапеции с углами 60º лежат в перпендикулярных плоскостях и имеют большее общее основание. Большие боковые стороны равны 4 см и 8 см. Найдите расстояние между вершинами прямых и вершинами тупых углов трапеций, если вершины их острых углов совпадают.

3.3. Задан куб ABCDA ₁ B ₁ C ₁ D ₁. Найдите угол между прямой CD ₁ и плоскостью BDC ₁.

3.4. На ребре АВ куба ABCDA ₁ B ₁ C ₁ D ₁ взята точка Р – середина этого ребра. Постройте сечение куба плоскостью, проходящей через точки C ₁, P, D, и найдите площадь этого сечения, если ребро куба равно а.

3.5. Через сторону AD прямоугольника ABCD проведена плоскость a так, что диагональ BD составляет с этой плоскостью угол 30º. Найдите угол между плоскостью прямоугольника и плоскостью a, если АВ = а, AD = b. Определите, при каком соотношении а и b задача имеет решение.

3.6. Найдите геометрическое место точек, равноудаленных от прямых, определенных сторонами треугольника.

Не нашли, что искали? Воспользуйтесь поиском: