Многогранники и тела вращения

Цилиндр называется описанным около призмы, если окружности оснований цилиндра описаны около оснований призмы, а боковые ребра призмы являются образующими цилиндра. Призма соответственно называется вписанной в цилиндр.

Теорема. Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

Цилиндр называется вписанным в призму, если окружности его оснований вписаны в основания призмы, а боковая поверхность касается боковых граней призмы.

Теорема. Для того чтобы в призму можно было вписать цилиндр, необходимо и достаточно, чтобы призма была прямая и в ее основание можно было вписать окружность.

Конус называется описанным около пирамиды, если окружность основания конуса описана около основания пирамиды, а боковые ребра пирамиды являются образующими конуса. Пирамида соответственно называется вписанной в конус.

Теорема. Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды были равны.

Конус называется вписанным в пирамиду, если окружность его основания вписана в основание пирамиды, а боковая поверхность касается боковых граней пирамиды. Пирамида соответственно называется описанной около конуса.

Теорема. Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы в основание пирамиды можно было вписать окружность, а вершина пирамиды ортогонально проектировалась в центр этой окружности.

Пример 1. Шар вписан в прямую призму, основанием которой является прямоугольный треугольник с катетом a и противолежащим ему острым углом α. Найти объем призмы.

Решение. Сделаем рисунок (рис. 12.48). Шар вписан в прямую призму, значит, высота призмы равна диаметру шара, а в треугольник основания вписана окружность, радиус которой равен радиусу шара. Рассмотрим прямоугольный треугольник ABC, у которого катет BC = a, противолежащий ему Ð BAC = α. Найдем катет AC и гипотенузу AB:

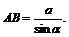
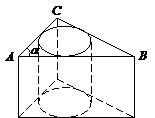
Рис. 12.48

Площадь треугольника ABC равна:

Вычислим радиус окружности, вписанной в треугольник:

Вычисляем объем призмы по формуле

Получаем ответ: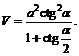

Пример 2. Боковое ребро правильной четырехугольной пирамиды равно a. Двугранный угол, образованный смежными боковыми гранями, равен β. Найти радиус шара, описанного около этой пирамиды.

Решение. Сделаем рисунок (рис. 12.49): ABCD – квадрат, SO – высота пирамиды, Ð AEC = b – двугранный угол.

Рассмотрим диагональное сечение пирамиды – треугольник SBD (SB = SD). Радиусом шара, описанного около данной пирамиды, будет радиус окружности, описанной около треугольника SBD. Найдем его по формуле

Рис. 12.49

Из подобия треугольников (Ð SOB = Ð SEO = 90°, Ð BSO = Ð OSE) следует пропорциональность сторон: SB / SO = BO / OE.

Из треугольника найдем 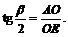Так как АО = ВО, то 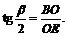Следовательно,

Вычисляем радиус окружности:

Получаем ответ: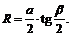

Пример 3. В усеченный конус вписан шар радиуса R. Образующая конуса наклонена к плоскости основания под углом a. Найти объем усеченного конуса.

Решение. Рассмотрим осевое сечение конуса (рис. 12.50).

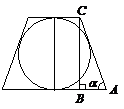
Рис. 12.50

Введем обозначения: R ₁ – радиус нижнего основания конуса, R ₂ – радиус верхнего основания. Высота данного усеченного конуса будет равна диаметру вписанного в него шара 2 R. Рассмотрим прямоугольный треугольник ABC: Ð B = 90°, Ð A = a, BC = 2 R. Найдем катет BA и гипотенузу AC: BA = BC × ctg a, Так как в усеченный конус вписан шар, то образующая этого конуса равна сумме радиусов его оснований. Получим равенство:

Заметим, что

Решив систему найдем

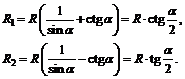
Вычисляем объем усеченного конуса по формуле (12.8).

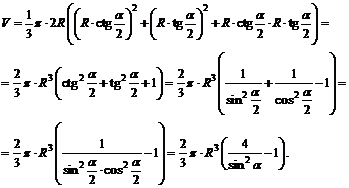
Получаем ответ:

Пример 4. В шар радиуса R вписан конус, образующая которого составляет с плоскостью основания угол φ. Найти площадь полной поверхности конуса.

Решение. Для вычисления площади полной поверхности конуса необходимо знать радиус основания и образующую конуса. Рассмотрим осевое сечение данного конуса – равнобедренный треугольник SAB: SA = SB – образующие, SD – высота, DB – радиус основания конуса (рис. 12.51).

Рис. 12.51

По условию задачи Ð SAD = φ, следовательно, Треугольник AOS – равнобедренный (AO = OS = R), поэтому Внешний угол этого треугольника при вершине О равен: Ð AOD = Ð SAO + Ð ASO = p – 2 j.

Из треугольника AOD (Ð D = 90°, AO = R, Ð AOD = p – 2 j) выразим AD:

Из треугольника ASD (Ð D = 90°, AD = R sin 2 j) выразим SA:

Подставив найденные выражения в формулу для вычисления площади полной поверхности конуса, получим:

Таким образом,

Пример 5. В прямой параллелепипед вписан цилиндр, объем которого в m раз меньше объема параллелепипеда. Найти двугранные углы при боковых ребрах параллелепипеда.

Решение. Двугранными углами при боковых ребрах данного параллелепипеда являются углы параллелограмма, лежащего в его основании. В параллелепипед вписан цилиндр, значит, в параллелограмм основания вписана окружность. Если в четырехугольник вписана окружность, то суммы длин противолежащих сторон четырехугольника равны. Таким образом, основанием параллелепипеда является ромб. Сделаем рисунок (рис. 12.52).

Рис. 12.52

Обозначим искомый угол a. Из треугольника ABC (Ð C = 90°, Ð A = a) найдем сторону ромба AB и его высоту BC:

Так как высоты цилиндра и параллелепипеда равны, то площадь основания цилиндра будет в m раз меньше площади основания параллелепипеда. Запишем равенство: 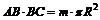и выразим из него далее

Двугранные углы при боковых ребрах параллелепипеда будут равны:

и

Задания

I уровень

1.1. В правильную четырехугольную пирамиду с объемом вписан конус. Найдите его объем.

1.2. В конус, образующая которого наклонена к плоскости основания под углом a, вписана пирамида. Основание пирамиды – прямоугольный треугольник с катетами 3 см и 4 см. Найдите объем пирамиды, если

1.3. Около цилиндра описана правильная четырехугольная призма, периметр основания которой равен 12 см, а площадь боковой поверхности равна 48 см². Найдите площадь полной поверхности цилиндра.

1.4. В равносторонний цилиндр, диагональ осевого сечения которого равна вписана правильная шестиугольная призма. Вычислите площадь боковой поверхности призмы.

1.5. Усеченный конус описан около правильной треугольной усеченной пирамиды. Радиус верхнего основания в 2 раза меньше радиуса нижнего основания конуса, высота равна 4 см, а образующая – 5 см. Найдите площадь боковой поверхности усеченной пирамиды.

1.6. В куб вписан шар и около куба описан шар. Найдите отношение объемов этих шаров.

1.7. В сферу вписан цилиндр. Площадь основания цилиндра равна 16 p см², тангенс угла наклона диагонали его осевого сечения к плоскости основания равен 3. Найдите площадь сферы.

1.8. В конус, площадь боковой поверхности которого в 2 раза больше площади основания, вписан шар. Найдите радиус шара, если образующая конуса равна 8 см.

1.9. В цилиндрическую мензурку, диаметр которой 2,5 см, заполненную водой до некоторого уровня, опускают четыре равных металлических шарика диаметром 1 см. Определите, на сколько изменится уровень воды в мензурке.

1.10. Основания шарового слоя и цилиндра совпадают. Объем тела, заключенного между их боковыми поверхностями, равен 36 p см³. Найдите высоту шарового слоя.

II уровень

2.1. Равносторонний треугольник, сторона которого равна а, вращается вокруг внешней оси, параллельной его высоте и удаленной от нее на Найдите площадь поверхности полученного тела вращения.

2.2. Усеченный конус вписан в четырехугольную усеченную пирамиду, основание которой – ромб со стороной а и углом a. Площадь боковой поверхности пирамиды равна S, боковые грани наклонены к основанию пирамиды под углом b. Найдите объем усеченного конуса.

2.3. В правильной треугольной призме боковое ребро равно стороне основания. Около призмы описан шар, а около шара описан конус. Образующая конуса равна l и составляет с плоскостью основания угол a. Найдите объем призмы.

2.4. В пирамиде, все боковые грани которой равнонаклонены к плоскости основания, через центр вписанного шара проведена плоскость, параллельная плоскости основания. Отношение площади сечения пирамиды этой плоскостью к площади основания равно k. Найдите угол между боковой гранью и основанием пирамиды.

2.5. В шар радиуса R вписаны два конуса с общим основанием. Вершины конусов совпадают с противоположными концами диаметра шара. Шаровой сегмент, вмещающий меньший конус, имеет в осевом сечении дугу a. Найдите расстояние между центрами шаров, вписанных в эти конусы.

2.6. Шар касается всех боковых ребер правильной четырехугольной призмы и ее оснований. Найдите отношение площади поверхности шара, лежащей вне призмы, к площади полной поверхности призмы.

2.7. В правильную четырехугольную пирамиду вписан равносторонний цилиндр так, что одна из его образующих расположена на диагонали основания пирамиды, а окружность основания касается двух смежных боковых граней пирамиды. Найдите радиус основания цилиндра, если боковое ребро пирамиды равно b, а угол его наклона к плоскости основания равен a.

2.8. Ребро тетраэдра равно 8 см. Цилиндрическая поверхность проходит через одно из его ребер и через все его вершины. Найдите радиус основания цилиндра.

2.9. Ребра треугольной пирамиды, выходящие из вершины S, попарно перпендикулярны и равны a, b и c. Найдите объем куба, вписанного в пирамиду так, что одна из его вершин совпадает с вершиной S пирамиды.

2.10. В усеченный конус вписан шар, объем которого составляет объема конуса. Найдите угол наклона образующей к плоскости нижнего основания конуса.

III уровень

3.1. Боковое ребро правильной треугольной пирамиды равно b и образует с плоскостью основания угол α. В пирамиду вписан равносторонний цилиндр так, что его нижнее основание лежит в плоскости основания пирамиды. Найдите высоту цилиндра.

3.2. Сфера с центром в вершине конуса касается его основания и делит поверхность конуса на две части, имеющие равные площади. Найдите угол при вершине осевого сечения конуса.

3.3. В куб, ребро которого равно a, вписан конус с углом между образующими в осевом сечении, равным α. Найдите длину образующей и радиус основания конуса, если его высота лежит на диагонали куба.

3.4. Шар касается трех граней куба, содержащих одну вершину, и проходит через вершину куба, противолежащую первой. Найдите радиус шара, если ребро куба равно a.

3.5. Цилиндр завершен сверху полушаром. Объем тела равен 45 π. При каком радиусе полушара полная поверхность тела будет наименьшей?

3.6. В конус с радиусом основания R и высотой H вписан цилиндр. Найдите линейные размеры цилиндра, при которых его объем будет наибольшим.

3.7. Найдите наибольший объем правильной шестиугольной пирамиды вписанной в шар, радиус которого равен R.

3.8. В правильную четырехугольную пирамиду вписан цилиндр так, что окружность его верхнего основания касается всех боковых граней пирамиды, а нижнее основание лежит в плоскости основания пирамиды. Какую часть высоты пирамиды должна составлять высота цилиндра, чтобы объем цилиндра был наибольшим?

Не нашли, что искали? Воспользуйтесь поиском: