Призма. Параллелепипед

Призмой называется многогранник, две грани которого – равные n -угольники (основания), лежащие в параллельных плоскостях, а остальные n граней – параллелограммы (боковые грани). Боковым ребром призмы называется сторона боковой грани, не принадлежащая основанию.

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой призмой (рис. 12.9). Если боковые ребра не перпендикулярны плоскостям оснований, то призма называется наклонной. Правильной призмой называется прямая призма, основания которой – правильные многоугольники.

Рис. 12.9

Высотой призмы называется расстояние между плоскостями оснований. Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани. Диагональным сечением называется сечение призмы плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Перпендикулярным сечением называется сечение призмы плоскостью, перпендикулярной боковому ребру призмы.

Площадью боковой поверхности призмы называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех граней призмы (т. е. сумма площадей боковых граней и площадей оснований).

Для произвольной призмы верны формулы:

(12.1)

где S_бок – площадь боковой поверхности; P – периметр перпендикулярного сечения; l – длина бокового ребра; S_полн – площадь полной поверхности; S_осн – площадь основания; V – объем призмы; H – высота; Q – площадь перпендикулярного сечения.

Для прямой призмы верны формулы:

где p – периметр основания; l – длина бокового ребра; H – высота.

Параллелепипедом называется призма, основанием которой служит параллелограмм. Параллелепипед, у которого боковые ребра перпендикулярны к основаниям, называется прямым (рис. 12.10). Если боковые ребра не перпендикулярны основаниям, то параллелепипед называется наклонным. Прямой параллелепипед, основанием которого является прямоугольник, называется прямоугольным. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.

 

Рис. 12.10

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. Длины ребер, исходящих из одной вершины, называются измерениями параллелепипеда. Так как параллелепипед – это призма, то основные его элементы определяются аналогично тому, как они определены для призм.

Теоремы:

1. Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

2. В прямоугольном параллелепипеде квадрат длины диагонали равен сумме квадратов трех его измерений:

3. Все четыре диагонали прямоугольного параллелепипеда равны между собой.

Для произвольного параллелепипеда верны формулы:

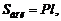
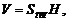
где S_бок – площадь боковой поверхности; P – периметр перпендикулярного сечения; l – длина бокового ребра; S_полн – площадь полной поверхности; S_осн – площадь основания; V – объем призмы; H – высота; Q – площадь перпендикулярного сечения.

Для прямого параллелепипеда верны формулы:

(12.2)

где p – периметр основания; l – длина бокового ребра; H – высота прямого параллелепипеда.

Для прямоугольного параллелепипеда верны формулы:

(12.3)

где p – периметр основания; H – высота; d – диагональ; a, b, c – измерения параллелепипеда.

Для куба верны формулы:

где d – диагональ куба; a – длина ребра.

 

Пример 1. Диагональ прямоугольного параллелепипеда равна 33 дм, а его измерения относятся, как 2: 6: 9. Найти измерения парал­лелепипеда.

Решение. Для нахождения измерений параллелепипеда воспользуемся формулой (12.3), т. е. тем фактом, что квадрат гипотенузы прямоугольного параллелепипеда равен сумме квадратов его измерений. Обозначим через k коэффициент пропорциональности. Тогда измерения параллелепипеда будут равны 2 k, 6 k и 9 k. Запишем формулу (12.3) для данных задачи:

т. е.

Решая это уравнение относительно k, получим:

Значит, измерения параллелепипеда равны 6 дм, 18 дм и 27 дм.

Пример 2. Найти объем наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной 8 см, если боковое ребро равно стороне основания и наклонено под углом 60º к основанию.

Решение. Сделаем рисунок (рис. 12.11).

Рис. 12.11

Для того чтобы найти объем наклонной призмы, необходимо знать площадь ее основания и высоту. Площадь основания данной призмы – это площадь равностороннего треугольника со стороной 8 см. Вычислим ее:

Высотой призмы является расстояние между ее основаниями. Из вершины А ₁ верхнего основания опустим перпендикуляр на плоскость нижнего основания А ₁ D. Его длина и будет высотой призмы. Рассмотрим D А ₁ АD: 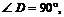так как это угол наклона бокового ребра А ₁ А к плоскости основания, А ₁ А = 8 см. Из этого треугольника находим А ₁ D:

Теперь вычисляем объем по формуле (12.1):

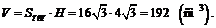
Получаем ответ: 192 см³.

Пример 3. Боковое ребро правильной шестиугольной призмы равно 14 см. Площадь наибольшего диагонального сечения равна 168 см². Найти площадь полной поверхности призмы.

Решение. Сделаем рисунок (рис. 12.12)

Рис. 12.12

Наибольшее диагональное сечение – прямоугольник AA ₁ D ₁ D, так как диагональ AD правильного шестиугольника ABCDEF является наибольшей. Для того чтобы вычислить площадь боковой поверхности призмы, необходимо знать сторону основания и длину бокового ребра.

Зная площадь диагонального сечения (прямоугольника), найдем диагональ основания.

Поскольку 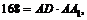то

Так как то АВ = 6 см.

Тогда периметр основания равен:

Найдем площадь боковой поверхности призмы:

Площадь правильного шестиугольника со стороной 6 см равна:

Находим площадь полной поверхности призмы:

Получаем ответ: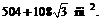

Пример 4. Основанием прямого параллелепипеда служит ромб. Площади диагональных сечений 300 см² и 875 см². Найти площадь боковой поверхности параллелепипеда.

Решение. Сделаем рисунок (рис. 12.13).

Рис. 12.13

Обозначим сторону ромба через а, диагонали ромба d ₁ и d ₂, высоту параллелепипеда h. Чтобы найти площадь боковой поверхности прямого параллелепипеда, необходимо периметр основания умножить на высоту: (формула (12.2)). Периметр основания р = АВ + ВС + + CD + DA = 4 AB = 4 a, так как ABCD – ромб. Н = АА ₁ = h. Таким образом Необходимо найти а и h.

Рассмотрим диагональные сечения. АА ₁ С ₁ С – прямоугольник, одна сторона которого диагональ ромба АС = d ₁, вторая – боковое ребро АА ₁ = h, тогда

Аналогично для сечения ВВ ₁ D ₁ D получим:

Используя свойство параллелограмма такое, что сумма квадратов диагоналей равна сумме квадратов всех его сторон, т. е. получаем:

Из первых двух равенств выразим 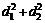и подставим в третье. Получим:

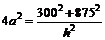и далее

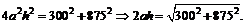
Тогда

Получаем ответ: 1850 см².

Пример 5. На ребрах СС ₁, AD и АВ куба ABCDA ₁ B ₁ C ₁ D ₁ взяты соответственно точки Р, М, R – середины этих ребер. Построить сечение куба плоскостью, проходящей через точки Р, М, R. Считая ребро куба равным 24 см, найти площадь полученного сечения.

Решение. Сделаем рисунок (рис. 12.14).

Рис. 12.14

Построение. Прямая MR – след секущей плоскости на плоскости нижнего основания. 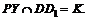Получается искомое сечение куба PNRMK. Для вычисления его площади воспользуемся теоремой о площади ортогональной проекции многоугольника на плоскость. Рассмотрим многоугольник PNRMK, его ортогональная проекция – СВRMD, определим, где угол между плоскостями этих многоугольников. Ребром двугранного угла является прямая MR. Из точки Р опустим перпендикуляр на прямую MR: точка Е – середина отрезка MR. 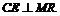– угол между плоскостью многоугольника и его проекцией. Теорему запишем в виде

Тогда

Вычислим 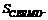Так как ABCD – квадрат, а треугольник – равнобедренный то

Вычислим

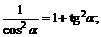
из

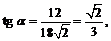
Площадь сечения:

Получаем ответ:

Задания

I уровень

1.1. Диагональ правильной четырехугольной призмы равна 25 см, а диагональ ее боковой грани – 20 см. Найдите высоту призмы.

1.2. Сечение железнодорожной насыпи имеет вид трапеции, нижнее основание которой 14 м, верхнее 8 м и высота 3,2 м. Определите, сколько кубических метров земли приходится на 1 км насыпи.

1.3. В наклонной треугольной призме проведено сечение, перпендикулярное боковому ребру, равному 12 см. В полученном треугольнике две стороны с длинами см и 8 см образуют угол 45°. Найдите площадь боковой поверхности призмы.

1.4. Основанием прямого параллелепипеда является ромб со стороной 4 см и острым углом 60°. Найдите диагонали параллелепипеда, если длина бокового ребра равна 10 см.

1.5. Основанием прямого параллелепипеда является квадрат с диагональю, равной 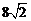см. Боковое ребро параллелепипеда 5 см. Найдите площадь полной поверхности параллелепипеда.

1.6. Основанием наклонного параллелепипеда является прямоугольник со сторонами 3 см и 4 см. Боковое ребро, равное см, наклонено к плоскости основания под углом 60°. Найдите объем параллелепипеда.

1.7. Вычислите площадь поверхности прямоугольного параллелепипеда, если два ребра и диагональ, исходящие из одной вершины, равны соответственно 11 см, см и 13 см.

1.8. Определите вес каменной колонны, имеющей форму прямоугольного параллелепипеда, с размерами 0,3 м, 0,3 м и 2,5 м, если удельный вес материала равен 2,2 г/см³.

1.9. Найдите площадь диагонального сечения куба, если диагональ его грани равна дм.

1.10. Найдите объем куба, если расстояние между двумя его вершинами, не лежащими в одной грани, равно 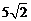см.

II уровень

2.1. Основанием наклонной призмы является равносторонний треугольник со стороной см. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите площадь сечения призмы, проходящего через боковое ребро и высоту призмы, если известно, что одна из вершин верхнего основания проектируется на середину стороны нижнего основания.

2.2. Основанием наклонной призмы является равносторонний треугольник ABC со стороной, равной 3 см. Вершина A ₁ проектируется в центр треугольника ABC. Ребро AA ₁ составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности призмы.

2.3. Вычислите объем наклонной треугольной призмы, если стороны основания 7 см, 5 см и 8 см, а высота призмы равна меньшей высоте треугольника-основания.

2.4. Диагональ правильной четырехугольной призмы наклонена к боковой грани под углом 30°. Найдите угол наклона к плоскости основания.

2.5. Основанием прямой призмы является равнобедренная трапеция, основания которой равны 4 см и 14 см, а диагональ – 15 см. Две боковые грани призмы – квадраты. Найдите площадь полной поверхности призмы.

2.6. Диагонали правильной шестиугольной призмы равны 19 см и 21 см. Найдите ее объем.

2.7. Найдите измерения прямоугольного параллелепипеда, у которого диагональ равна 8 дм, и она образует с боковыми гранями углы 30° и 40°.

2.8. Диагонали основания прямого параллелепипеда равны 34 см и 38 см, а площади боковых граней – 800 см² и 1200 см². Найдите объем параллелепипеда.

2.9. Определите объем прямоугольного параллелепипеда, в котором диагонали боковых граней, выходящие из одной вершины, равны 4 см и 5 см и образуют угол 60°.

2.10. Найдите объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно 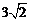мм.

III уровень

3.1. В правильной треугольной призме проведено сечение через сторону основания и середину противоположного бокового ребра. Площадь основания равна 18 см², а диагональ боковой грани наклонена к основанию под углом 60°. Найдите площадь сечения.

3.2. В основании призмы лежит квадрат ABCD, все вершины которого равноудалены от вершины A ₁ верхнего основания. Угол между боковым ребром и плоскостью основания равен 60°. Сторона основания – 12 см. Постройте сечение призмы плоскостью, проходящей через вершину C, перпендикулярно ребру AA ₁, и найдите его площадь.

3.3. Основанием прямой призмы является равнобедренная трапеция. Площадь диагонального сечения и площади параллельных боковых граней соответственно равны 320 см², 176 см² и 336 см². Найдите площадь боковой поверхности призмы.

3.4. Площадь основания прямой треугольной призмы равна 9 см², площади боковых граней 18 см², 20 см² и 34 см². Найдите объем призмы.

3.5. Найдите диагонали прямоугольного параллелепипеда, зная, что диагонали его граней равны 11 см, 19 см и 20 см.

3.6. Углы, образованные диагональю основания прямоугольного параллелепипеда со стороной основания и диагональю параллелепипеда, равны соответственно a и b. Найдите площадь боковой поверхности параллелепипеда, если его диагональ равна d.

3.7. Площадь того сечения куба, которое представляет собой правильный шестиугольник, равна см². Найдите площадь поверхности куба.

3.8. Измерения одного прямоугольного параллелепипеда относятся как 3: 5: 6, а измерения второго – как 3: 6: 7. Зная, что их площади полных поверхностей относятся как 7: 9, найдите отношения объемов.

3.9. Основанием наклонного параллелепипеда является ромб со стороной, равной b, и углом 60°. Боковое ребро также равно b и образует с прилежащими сторонами основания углы по 45°. Найдите объем параллелепипеда.

Не нашли, что искали? Воспользуйтесь поиском: