Шаровой слой и сферический пояс

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. Круги, получившиеся в сечении, называются основаниями слоя. Расстояние между секущими плоскостями называется высотой слоя (рис. 12.42). Поверхность сферической части шарового слоя называется сферическим поясом.

Шар, шаровой сегмент и шаровой слой можно рассматривать как геометрические тела вращения. При вращении полукруга вокруг оси, содержащей диаметр полукруга, получается шар, соответственно при вращении частей круга получаются части шара: шаровой сегмент и шаровой слой.

Рис. 12.42

Для шарового слоя верны формулы:

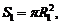
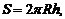
где S ₁, S ₂ – площади оснований; R ₁, R ₂ – радиусы оснований; S – площадь сферической части шарового слоя (площадь сферического пояса); R – радиус шара; h – высота; S_полн – площадь полной поверхности; V – объем шарового слоя.

Шаровой сектор

Шаровым сектором называется геометрическое тело, полученное при вращении кругового сектора (с углом меньше 90°) вокруг оси, содержащей один из боковых радиусов. Дополнение такого тела до шара также называется шаровым сектором. Таким образом, шаровой сектор состоит из шарового сегмента и конуса, либо из шарового сегмента без конуса (рис. 12.43 а, б).

а) б)

Рис. 12.43

Для шарового сектора верны формулы:

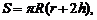
где S – площадь поверхности шарового сектора; R – радиус шара; r – радиус основания сегмента; h – высота шарового сегмента; V – объем шарового сектора.

Пример 1. Радиус шара разделили на три равные части. Через точки деления провели два сечения, перпендикулярные радиусу. Найти площадь сферического пояса, если радиус шара равен 15 см.

Решение. Сделаем рисунок (рис. 12.44).

Рис. 12.44

Для того чтобы вычислить площадь сферического пояса, надо знать радиус шара и высоту. Радиус шара известен, а высоту найдем, зная, что радиус разделен на три равные части:

Тогда площадь

Пример 2. Шар пересечен двумя параллельными плоскостями, проходящими перпендикулярно диаметру и по разные стороны от центра шара. Площади сферических сегментов равны 42 p см² и 70 p см². Найти радиус шара, если расстояние между плоскостями равно 6 см.

Решение. Рассмотрим два сферических сегмента с площадями: где R – радиус шара (сферы), h, H – высоты сегментов. Получим уравнения: и Имеем два уравнения с тремя неизвестными. Составим еще одно уравнение. Диаметр шара равен Решим систему:

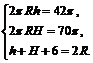
Из двух первых уравнений системы выражаем:

подставляем в третье уравнение системы: Решаем полученное уравнение: 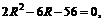получаем

По условию задачи подходит значение

Пример 3. Сечение шара плоскостью, перпендикулярной его диаметру, делит диаметр в отношении 1: 2. Во сколько раз площадь сечения меньше площади поверхности шара?

Решение. Сделаем рисунок (рис. 12.45).

Рассмотрим диаметральное сечение шара: AD – диаметр, O – центр, OE=R – радиус шара, BE – радиус сечения, перпендикулярного диаметру шара,

Выразим BE через R: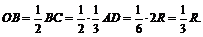

Из D OBE выразим BE через R:

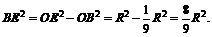
Рис. 12.45

Площадь сечения 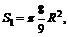площадь поверхности шара Получаем отношение

Следовательно, S ₁меньше S ₂в 4,5 раза.

Пример 4. В шаре, радиус которого 13 см, проведены два взаимно перпендикулярных сечения на расстоянии 4 см и 12 см от центра. Найти длину их общей хорды.

Решение. Сделаем рисунок (рис. 12.46).

Рис. 12.46

Сечения перпендикулярны, так как 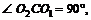OO ₂ – расстояние и OO ₁ – расстояние. Таким образом, и OC – диагональ прямоугольника OO ₂ CO ₁ и равна

D O ₁ AB – равнобедренный (O ₁ A = O ₁ B – радиусы), тогда перпендикуляр O ₁ C является и медианой AC = CB.

Рассмотрим D OAC: OA – радиус шара, (OC ^ AC по теореме о трех перпендикулярах). Находим:

Общая хорда сечений

Получаем ответ: 6 см.

Пример 5. Площадь осевого сечения шарового сектора в три раза меньше площади большого круга шара. Найти отношение объемов сектора и шара.

Решение. Сделаем рисунок (рис. 12.47).

Рис. 12.47

Рассмотрим осевое сечение шара. Осевое сечение шарового сектора – это круговой сектор, площадь которого составляет площади круга. Значит, центральный угол равен 120°, следовательно, Шаровой сектор можно рассматривать как тело, полученное при вращении сектора АОВ вокруг бокового радиуса ОВ. Высотой данного сектора служит отрезок СВ. Объем сектора вычисляется по формуле объем шара –

Из D АОС ( ОА – радиус) выразим Таким образом, Следовательно, Сравнивая объемы сектора и шара, получаем, что V_c: V_ш = 1: 4.

Получаем ответ: 1: 4.

Задания

I уровень

1.1. В шаре на расстоянии 9 см от центра проведено сечение, площадь которого равна 144 p см². Найдите радиус шара.

1.2. Два равных шара радиусом R = 17 см, взаимно пересекаясь, образуют двояковыпуклую линзу. Найдите ее диаметр, если расстояние между центрами шаров равно R.

1.3. Найдите высоту шарового сегмента, если радиус его основания равен 15 см, а радиус шара – 25 см.

1.4. Шар, радиус которого 15 см, пересечен плоскостью на расстоянии 9 см от центра. Найдите площадь сферической части шарового сегмента.

1.5. Найдите площадь сферы, диаметр которой равен диагонали куба с ребром, равным 2 см.

1.6. Определите, во сколько раз объем Земли больше объема Луны. (Диаметр Земли следует принять за 13 тыс. км, диаметр Луны – 3,5 тыс. км.)

1.7. Объем стенок полого шара равен 876 p см³, а толщина стенок – 3 см. Найдите радиусы наружной и внутренней поверхностей шара.

1.8. Найдите объем шарового сектора, если радиус шара равен 10 см, а радиус основания соответствующего шарового сегмента – 6 см.

1.9. Объем одного шара в 8 раз больше объема другого шара. Определите, во сколько раз площадь поверхности первого шара больше площади поверхности второго.

II уровень

2.1. Стороны треугольника, равные 5 см, 5 см и 6 см, касаются шара, радиус которого 2,5 см. Найдите расстояние от центра шара до плоскости треугольника.

2.2. На поверхности шара даны три точки. Расстояния между ними равны по 7 см. Радиус шара равен 7 см. Найдите расстояние от центра шара до плоскости, проходящей через данные три точки.

2.3. Радиусы оснований шарового слоя равны 63 см и 39 см, его высота – 36 см. Найдите радиус шара.

2.4. Дан шар радиуса 12 см. Через одну точку его поверхности проведены две плоскости: первая поверхность касается шара, вторая – под углом 60° к радиусу, проведенному в точку касания. Найдите площадь сечения.

2.5. Определите, какую площадь имеет часть поверхности шара, которая видна наблюдателю, находящемуся на расстоянии 10 м от него, если радиус воздушного шара равен 15 м.

2.6. Шар пересечен двумя плоскостями, проходящими через одну точку поверхности шара и образующими угол 60°. Радиус шара равен 4 см. Найдите площади поверхностей отсекаемых сегментов, если окружности их оснований имеют равные радиусы.

2.7. Шар касается граней двугранного угла в 120°. Расстояние от центра шара до ребра угла равно 10 см. Найдите площадь поверхности шара.

2.8. Из шара вырезали шаровой слой, толщина которого равна 9 см, площади оснований – 400 p см² и 49 p см². Найдите объемы оставшихся шаровых сегментов.

2.9. Диаметр шара разделен на четыре равные части и через точки деления проведены секущие плоскости, перпендикулярные диаметру. Найдите объемы полученных частей шара, если его радиус равен R.

2.10. В шаре радиуса R просверлено цилиндрическое отверстие. Ось цилиндра проходит через центр шара, диаметр отверстия равен радиусу шара. Найдите объем оставшейся части шара.

III уровень

3.1. Плоскости двух сечений шара взаимно перпендикулярны. Одна из этих плоскостей проходит через центр шара, другая – удалена от него на 12. Общая хорда сечений равна 18. Найдите сумму площадей этих сечений.

3.2. Радиус шара равен 15 м. Вне шара дана точка А на расстоянии 10 м от его поверхности. Найдите радиус такой окружности на поверхности шара, все точки которой отстоят от точки А на 20 м.

3.3. Из точки, взятой на поверхности шара, проведены три равные хорды, угол между каждой парой которых равен a. Найдите длину хорды, если радиус шара равен R.

3.4. Два шара внутренне касаются в точке А, АВ – диаметр большего из шаров, ВС – касательная к меньшему из них. Найдите радиусы шаров, если ВС = 20 см, а разность площадей поверхностей шаров равна 700 p см².

3.5. Вычислите объем шара, радиус которого равняется ребру октаэдра, имеющего поверхность площадью

3.6. Круговой сектор с углом 60° и радиусом R вращается около одного из боковых радиусов. Найдите объем полученного тела вращения.

Не нашли, что искали? Воспользуйтесь поиском: