Пирамида. Усеченная пирамида

Пирамидой называется многогранник, одна из граней которого – многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 12.15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 12.16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.

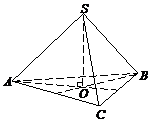Рис. 12.15 Рис. 12.16

Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию. Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.

Теоремы:

1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности, описанной около основания.

2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности, описанной около основания.

3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности, вписанной в основание.

Для вычисления объема произвольной пирамиды верна формула:

где V – объем; S_осн – площадь основания; H – высота пирамиды.

Для правильной пирамиды верны формулы:

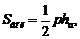
где S_бок – площадь боковой поверхности; p – периметр основания; h_а – апофема; S_полн – площадь полной поверхности; S_осн – площадь основания; V – объем правильной пирамиды; H – высота.

Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 12.17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.

Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Рис. 12.17

Для усеченной пирамиды справедливы формулы:

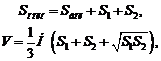(12.4)

где S_полн – площадь полной поверхности; S_бок – площадь боковой поверхности; S ₁, S ₂ – площади верхнего и нижнего оснований; V – объем усеченной пирамиды; H – высота.

Для правильной усеченной пирамиды верна формула:

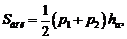
где p ₁ , p ₂ – периметры оснований; h_а – апофема правильной усеченной пирамиды.

Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.

Решение. Сделаем рисунок (рис. 12.18).

Рис. 12.18

Пирамида правильная, значит в основании лежит равносторонний треугольник и все боковые грани – равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т. е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3 а. Точкой О отрезок BD делится на части: 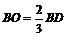и Из находим SO:

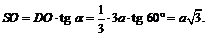
Из находим:

Получаем ответ: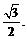

Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и 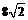см, а высота – 4 см.

Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (12.4). Чтобы найти площади оснований, необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит, площади оснований равны и 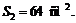Подставив все данные в формулу, вычислим объем усеченной пирамиды:

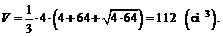
Получаем ответ: 112 см³.

Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды – 2 см.

Решение. Сделаем рисунок (рис. 12.19).

Рис. 12.19

Боковой гранью данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из 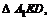где А ₁ Е – перпендикуляр из точки А ₁ на плоскость нижнего основания, A ₁ D – перпендикуляр из точки А ₁ на АС. А ₁ Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 12.20). Точка О – проекция центров верхнего и нижнего оснований. 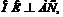так как (рис. 12.20) и С другой стороны, ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:

Рис. 12.20

MK = DE.

По теореме Пифагора из

Площадь боковой грани:

Получаем ответ:

Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол, равный j. Найти площадь полной поверхности пирамиды.

Решение. Сделаем рисунок (рис. 12.21).

Рис. 12.21

Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD.

Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры имеем:

откуда получаем:

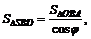
Аналогично и, значит, Таким образом, задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис. 12.22). Точка О – центр вписанной в трапецию окружности.

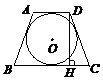
Рис. 12.22

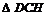Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем:

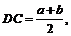
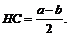
Тогда

Площадь трапеции: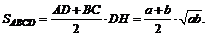

Следовательно,

Получаем ответ:

Пример 5. Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.

Решение. Сделаем рисунок (рис. 12.23).

Рис. 12.23

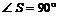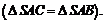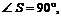
Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( ), два других – равные треугольники Рассмотрим – по условию. Вычислим его площадь: Так как 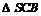равнобедренный, то 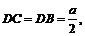а так как 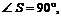то и, следовательно, в

Тогда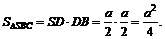

Рассмотрим SE найдем из По теореме Пифагора имеем Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 12.24). 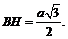В отрезок DE является средней линией, следовательно, Находим SE:

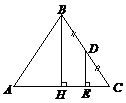
Рис. 12.24

Теперь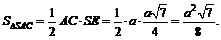

Площадь боковой поверхности пирамиды равна:

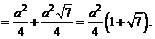
Получаем ответ:

Задания

I уровень

1.1. Боковое ребро правильной четырехугольной пирамиды равно диагонали основания, длина которой 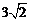см. Найдите высоту пирамиды и сторону ее основания.

1.2. Основанием пирамиды является треугольник со сторонами 6 см, 8 см и 10 см. Боковые грани наклонены к плоскости основания под углом 60º. Найдите высоту пирамиды.

1.3. Найдите площадь полной поверхности правильной шестиугольной пирамиды, зная, что апофема равна 10 см, а радиус окружности, описанной около основания, равен 6 см.

1.4. Найдите высоту правильной четырехугольной пирамиды, сторона которой 6 см, если ее объем равен объему куба со стороной 4 см.

1.5. Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны b. Найдите объем пирамиды.

1.6. Стороны оснований правильной усеченной четырехугольной пирамиды равны 8 см и 4 см. Боковое ребро равно см. Найдите высоту пирамиды.

1.7. Боковые ребра правильной усеченной шестиугольной пирамиды наклонены к плоскости нижнего основания под углом 45º. Стороны оснований равны 10 см и 5 см. Найдите длину бокового ребра и высоту пирамиды.

1.8. Боковая грань правильной семиугольной усеченной пирамиды – равнобедренная трапеция, средняя линия которой равна 13 см, а высота – 8 см. Вычислите площадь боковой поверхности пирамиды.

1.9. Площадь полной поверхности правильной треугольной усеченной пирамиды равна см². Стороны оснований – 10 см и 6 см. Найдите тангенс угла между боковым ребром и стороной нижнего основания.

1.10. В правильной усеченной четырехугольной пирамиде стороны оснований равны 5 см и 17 см, боковые грани наклонены к плоскости основания под углом 45º. Вычислите объем пирамиды.

II уровень

2.1. По стороне основания, равной 5 см, и высоте, равной 12 см, найдите апофему и боковое ребро правильной шестиугольной пирамиды.

2.2. Найдите расстояние между центрами окружностей, вписанных в смежные боковые грани тетраэдра. Радиус окружности равен дм.

2.3. Основание пирамиды – ромб со стороной 6 см и углом 45º, все двугранные углы при сторонах основания пирамиды равны 30º. Вычислите площадь полной поверхности пирамиды.

2.4. В правильной треугольной пирамиде боковое ребро равно 8 см, а плоский угол при вершине – 30º. Найдите площадь полной поверхности пирамиды.

2.5. Одно из самых грандиозных сооружений древности – пирамида Хеопса – имеет форму правильной четырехугольной пирамиды высотой» 150 м и боковым ребром» 220 м. Найдите объем этой пирамиды.

2.6. Определите объем правильной треугольной пирамиды, если боковая грань наклонена к плоскости основания под углом 60º и удалена от противоположной вершины на расстояние, равное 3 см.

2.7. В правильной четырехугольной усеченной пирамиде стороны оснований равны 15 дм и 5 дм. Площадь диагонального сечения равна 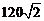дм². Найдите площадь полной поверхности пирамиды.

2.8. Основания усеченной пирамиды – равнобедренные треугольники, их равные стороны – 8 см и 4 см, углы при вершинах треугольников равны по 120º. Ребро, проходящее через вершины данных углов, перпендикулярно плоскости оснований и равно 3 см. Вычислите площадь боковой поверхности пирамиды.

2.9. Правильная четырехугольная пирамида, сторона основания которой 1500 см и высота 2000 см, пересечена плоскостью, параллельной основанию. Найдите объем усеченной пирамиды, если ее высота равна 1400 см.

2.10. В правильной усеченной треугольной пирамиде стороны оснований равны 7 см и 3 см, а апофема – 5 см. Найдите объем пирамиды.

III уровень

3.1. Основанием пирамиды является равносторонний треугольник. Одна из боковых граней пирамиды перпендикулярна плоскости основания, две другие образуют с плоскостью основания угол a. Найдите косинус угла между этими гранями.

3.2. Все диагональные сечения правильной шестиугольной пирамиды SABCDEF равновелики. Найдите угол между плоскостью основания и плоскостью сечения SAC.

3.3. Точка М – середина ребра SB пирамиды SABC, основанием которой является правильный треугольник ABC, а боковое ребро SC перпендикулярно плоскости ABC и SC = 2 AB. Найдите расстояние от точки М до прямой AC, если АВ = а.

3.4. Основанием пирамиды служит ромб со стороной а и острым углом a. Две боковые грани перпендикулярны основанию, а две другие наклонены к нему под углом j. Найдите площадь боковой поверхности пирамиды.

3.5. Основанием пирамиды является равнобокая трапеция, острый угол которой a, а площадь Q. Каждая боковая грань образует с основанием угол b. Найдите объем пирамиды.

3.6. Основание усеченной пирамиды – прямоугольник со сторонами 6 см и 8 см. Одно из боковых ребер перпендикулярно плоскости основания и равно 7 см. Вершина верхнего основания проектируется в точку пересечения диагоналей нижнего основания. Найдите длины остальных боковых ребер и угол наклона большего бокового ребра к плоскости основания.

3.7. Основания усеченной пирамиды – квадраты со сторонами 8 см и 4 см. Одна из боковых граней перпендикулярна плоскости основания и является равнобедренной трапецией. Противолежащая ей грань образует с плоскостью основания угол 60º. Найдите площади боковых граней пирамиды.

3.8. Стороны оснований и высота правильной четырехугольной усеченной пирамиды относятся как 7: 4: 2, площадь боковой поверхности равна 110 дм². Вычислите площадь полной поверхности пирамиды.

3.9. Найдите объем правильной треугольной усеченной пирамиды, у которой стороны оснований равны 3 м и 2 м, а площадь боковой поверхности равна сумме площадей оснований.

3.10. Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 см и 1 см, высота – 3 см. Через точку пересечения диагоналей пирамиды, параллельно основаниям пирамиды, проведена плоскость, делящая пирамиду на две части. Найдите объем каждой из полученных частей.

Цилиндр

Цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой параллельно данной прямой (рис. 12.25).

Данная кривая называется направляющей, а прямые – образующими цилиндрической поверхности.

Прямой круговой цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности перпендикулярно плоскости этой окружности. В дальнейшем эту поверхность будем кратко называть цилиндрической (рис. 12.26).

Цилиндром (прямым круговым цилиндром) называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим поверхности (рис. 12.27).

Рис. 12.25 Рис. 12.26 Рис. 12.27

Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг оси, содержащей одну из сторон прямоугольника.

Два круга, ограничивающие цилиндр, называются его основаниями. Прямая, проходящая через центры данных кругов, называется осью цилиндра. Отрезки, образующие цилиндрическую поверхность, называются образующими цилиндра. Высотой цилиндра называется расстояние между его основаниями. Осевым сечением называется сечение, проходящее через ось цилиндра. Разверткой боковой поверхности цилиндра называется прямоугольник со сторонами, равными длине окружности основания и длине образующей цилиндра.

Для цилиндра верны формулы:

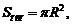
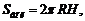
(12.5)

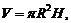(12.6)

где S_осн – площадь основания; R – радиус основания; S_бок – площадь боковой поверхности; H – высота; S_полн – площадь полной поверхности; V – объем цилиндра.

Пример 1. Найти радиус основания цилиндра, если его высота равна 8 см, а диагональ осевого сечения составляет угол 45º с плоскостью основания.

Решение. Сделаем рисунок (рис. 12.28).

Рис. 12.28

Осевое сечение цилиндра – это прямоугольник, одна сторона которого – образующая (высота) цилиндра, вторая сторона – диаметр основания цилиндра. Рассмотрим треугольник АВС, у которого катетами являются диаметр основания АС и высота ВС, а гипотенузой – диагональ сечения АВ. Так как то – равнобедренный и АС = ВС = 8 см. АС – диаметр, значит, радиус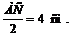

Получаем ответ: 4 см.

Пример 2. Цилиндр пересечен плоскостью, параллельной оси. Найти площадь сечения, если радиус основания и высота цилиндра соответственно равны 5 см и 10 см, а расстояние от оси цилиндра до плоскости сечения – 3 см.

Решение. Сделаем рисунок (рис. 12.29).

Рис. 12.29

Сечением цилиндра является прямоугольник, одна из сторон которого – хорда окружности основания (ВС), вторая – образующая цилиндра (ВА). Образующая равна высоте, значит ВА = 10 см. Необходимо найти хорду ВС. Расстояние от оси ОО ₁ до плоскости сечения – это перпендикуляр, опущенный из точки О ₁ на хорду ВС. Проведя радиусы О ₁ С и О ₁ В, получим равнобедренный треугольник Высота O ₁ D является его медианой, значит BD = DC. Из 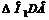найдем BD:

Тогда BC = 2 BD = 8 см. Площадь сечения:

Получаем ответ: 80 см².

Пример 3. Диагональ сечения цилиндра, параллельного его оси, равна d и образует угол a с образующей цилиндра. Найти площадь полной поверхности цилиндра, если секущая плоскость отсекает от окружности основания часть.

Решение. Сделаем рисунок (рис. 12.30).

Рис. 12.30

Площадь полной поверхности цилиндра вычисляется по формуле (12.5).

Чтобы найти высоту Н (образующую), рассмотри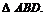м В нем Тогда

Для нахождения радиуса рассмотрим равнобедренный в котором OA = OD = R. Так как по условию сечение отсекает от окружности основания часть, значит По теореме косинусов найдем радиус:

т. е.

Тогда откуда получаем:

Вычисляем:

Получаем ответ:

Пример 4. Диагонали развертки боковой поверхности цилиндра образуют острый угол, равный a. Высота цилиндра равна h. Найти объем цилиндра.

Решение. Сделаем рисунок (рис. 12.31).

Рис. 12.31

Чтобы найти объем, необходимо знать радиус основания цилиндра. Рассмотрим развертку боковой поверхности цилиндра – прямоугольник ABCD: AD = h, BC = 2 pR,где R – неизвестный радиус основания. Точка О – середина диагоналей. Из точки О опустим перпендикуляр OD, и вычислим:

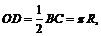с другой стороны

Приравнивая выражения для нахождения OD, находим R:

т. е.

Вычисляем объем цилиндра по формуле (12.6):

Получаем ответ:

Задания

I уровень

1.1. Найдите диагональ осевого сечения цилиндра, высота которого равна 8 см, а радиус основания – 3 см.

1.2. Осевое сечение цилиндра – квадрат, площадь которого 64 см². Найдите площадь основания цилиндра.

1.3. Площадь осевого сечения цилиндра равна S. Найдите площадь его боковой поверхности.

1.4. Высота цилиндра равна 12 см, диагональ осевого сечения – 13 см. Найдите площадь боковой поверхности цилиндра.

1.5. Диагональ осевого сечения цилиндра равна см и составляет угол 45º с плоскостью основания. Найдите площадь боковой поверхности цилиндра.

1.6. Цилиндр образован вращением прямоугольника вокруг меньшей из сторон. Найдите площадь полной поверхности цилиндра, если диагональ прямоугольника равна 6 см и наклонена к большей стороне под углом 30º.

1.7. Определите давление кирпичной цилиндрической колонны на фундамент, если высота колонны равна 2 м, диаметр основания равен 0,75 м. Вес одного кубического метра кирпича необходимо принять равным 1,8 т.

1.8. Развертка боковой поверхности цилиндра – квадрат со стороной 18 см. Найдите объем цилиндра.

1.9. Как изменится объем цилиндра, если радиус основания увеличить в три раза, а высоту уменьшить в четыре раза?

1.10. Два различных цилиндра имеют равные площади боковых поверхностей. Найдите отношение радиусов оснований, если их высоты относятся как 3: 1.

II уровень

2.1. Цилиндр, радиус основания которого равен 13 см, а высота – 10 см, пересечен плоскостью так, что в сечении получился квадрат. Определите, на каком расстоянии от оси цилиндра проведено сечение.

2.2. Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площадь каждого из полученных сечений равна 71 дм². Найдите площадь осевого сечения цилиндра.

2.3. Радиус основания цилиндра в три раза меньше его высоты. Найдите угол между диагоналями осевого сечения цилиндра.

2.4. Цилиндрическая дымовая труба диаметром 60 см имеет высоту 20 м. Определите, сколько квадратных метров листового железа потребуется на ее изготовление, если на заклепки уходит 10 % всего необходимого количества железа.

2.5. Развертка боковой поверхности цилиндра – квадрат. Найдите объем цилиндра, если радиус его основания на 3 см меньше высоты.

2.6. Площадь основания цилиндра равновелика площади развертки его боковой поверхности. Найдите тангенс угла наклона диагонали осевого сечения к плоскости основания цилиндра.

2.7. Прямоугольник со сторонами m и b является разверткой боковых поверхностей двух различных цилиндров. Найдите отношение объемов этих цилиндров.

2.8. Кусок льда, имеющий форму прямоугольного параллелепипеда, размером 0,6 м ´ 0,4 м ´ 0,5 м, помещен в цилиндрический сосуд диаметра 0,9 м. Определите, какова будет высота слоя воды после того, как лед растает. Удельный вес льда необходимо считать равным 0,92 г/см³.

III уровень

3.1. Точка окружности верхнего основания цилиндра соединена с точкой окружности нижнего основания. Угол между радиусами, проведенными в эти точки, равен a. Найдите угол между осью цилиндра и отрезком, соединяющим данные точки, если высота цилиндра равна его диаметру.

3.2. К цилиндру проведена касательная прямая под углом a к плоскости основания. Определите расстояние от центра нижнего основания до прямой, если расстояние от центра до точки касания равно d, а радиус основания равен R.

3.3. Высота цилиндра равна радиусу его основания и имеет длину а. Через ось цилиндра проведена вторая цилиндрическая поверхность, которая делит окружность основания на две дуги, длины которых относятся как 2: 1. Найдите объем большей части цилиндра, на которые цилиндрическая поверхность делит цилиндр.

3.4. Два равных цилиндра, высоты которых больше их диаметров, расположены так, что их оси пересекаются под прямым углом и точка пересечения осей равноудалена от оснований цилиндров. Найдите объем общей части этих цилиндров, если радиус каждого из них равен 1 см.

Не нашли, что искали? Воспользуйтесь поиском: