ВЕКТОРЫ И КООРДИНАТЫ

А.Д. Ходалевич

Р.В. Бородич

В.Н. Рыжик

«Аналитическая геометрия»

Тексты лекций

Гомель, 2004

УДК 514 (078)

ББК 22.151 Я73

Х 69

Рецензенты: Семенчук В.Н. – профессор, доктор физико-математических наук кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».

Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7

Ходалевич А.Д.

Х 69 Аналитическая геометрия: Тексты лекций. /А.Д.Ходалевич,

Р.В.Бородич, В.Н. Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины»; 2004 − 65с.

Дается краткое изложение курса лекций по аналитической геометрии для студентов, обучающихся по специальности «Прикладная математика»

УДК 514 (078)

ББК 22.151 Я73

Х 69

© А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик, 2004

© Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2004

СОДЕРЖАНИЕ

1. Векторы и координаты………………………………….…4

2. Прямая на плоскости………………………………………20

3. Плоскость…………………………………………………...25

4. Прямая в пространстве. Взаимное расположение

прямой и плоскости в пространстве…………………………29

5. Кривые второго порядка…………………………………...33

6. Поверхности второго порядка……………………………..56

Литература………………………………………………….….64

Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических мето­дов, в основе которых лежит понятие координат.

ВЕКТОРЫ И КООРДИНАТЫ

Понятие вектора

Пусть А – произвольное непустое множество. Декартовым кваратом А называется множество

A ² =

Бинарным отношением на А называется любое подмножество множества A ².

Отношением эквивалентности на А называется такое бинарное отношение на А, которое удовлетворяет следующим условиям:

1) 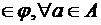(рефлексивность);

2) если (,b) то (b, ) (симметричность);

3) если (,b) то (,c) (транзитивность).

Теорема. Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.

Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается .

Пусть заданы направленные отрезки и 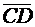, не лежащие на двух различных параллельных прямых, и плоскость , проходящая через точки В и D. Тогда плоскость разбивает все пространство на два полупространства. Если при этом точки B и D лежат в одном полупространстве, то говорят, что направленные отрезки и 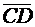одинаково направлены (обозначается ). В противном случае, они называются противоположно направленными (обозначается ).

Если направленные отрезки и 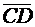лежат на одной прямой, то они одинаково (противоположно) направлены, если существует такой третий направленный отрезок , который одинаково направлен с каждым из направленных отрезков и 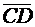(противоположно направлен в точности с одним из направленных отрезков или ).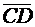

Абсолютной величиной или модулем (длиной) направленного отрезка называется длина этого направленного отрезка и обозначается | |.

Два направленных отрезка и называются равными, если и 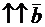, при этом пишут = ,

Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.

Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности.

Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.

Векторы и называются коллинеарными, если образующие их направленные отрезки параллельны одной и той же прямой (обозначается || ).

Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости.

Нулевым вектором называется вектор, начало которого совпадает с его концом (обозначается ). Направление нулевого вектора не определено.

Не нашли, что искали? Воспользуйтесь поиском: