
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Скалярное произведение векторов. Определение. Скалярнымпроизведениемвекторов и называется число (которое обозначается ), равное произведению длин этих векторов на косинус угла между ними
Определение. Скалярнымпроизведениемвекторов  и
и  называется число (которое обозначается
называется число (которое обозначается 
 ), равное произведению длин этих векторов на косинус угла между ними, т.е.
), равное произведению длин этих векторов на косинус угла между ними, т.е.
 .
.
Из первого пункта предыдущей теоремы сразу следует, что
 .
.
Так как соs 0 = 1. то 
 =|
=|  |2. Следовательно,
|2. Следовательно,
 ,
,
где выражение  ×
×  =
=  2 называется скалярным квадратом вектора
2 называется скалярным квадратом вектора  .
.
Теорема. Скалярное произведение двух векторов обладает следующими свойствами:
1)  ×
×  =
=  ×
×  (коммутативность);
(коммутативность);
2) λ (
 ) = (λ
) = (λ  )
)  ,
, 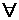 λ
λ  R;
R;
3)  (
( +
+ 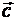 ) =
) = 
 +
+ 
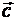 (дистрибутивность).
(дистрибутивность).
Из определения следует, что
 .
.
Tеорема (необходимое и достаточное условие ортогональности двух векторов). Два ненулевых вектора взаимно перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю.
Не нашли, что искали? Воспользуйтесь поиском: