
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Линейные операции над векторами.
Определение. Суммой  +
+  векторов
векторов  и
и  называется вектор, проведенный из начала
называется вектор, проведенный из начала  к концу
к концу  , если конец
, если конец  и начало
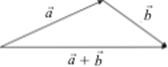
и начало  совпадают. Приведенное определение сложения векторов называется правилом треугольника. Векторы
совпадают. Приведенное определение сложения векторов называется правилом треугольника. Векторы  и
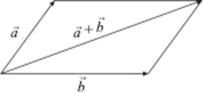
и  можно складывать, пользуясь правилом параллелограмма.
можно складывать, пользуясь правилом параллелограмма.
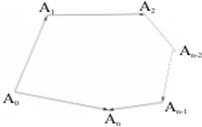
Если имеется n векторов 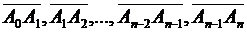 , то их сумма определяется как вектор
, то их сумма определяется как вектор 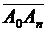 .
.
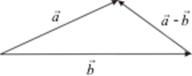
Определение. Разностью векторов  и
и  называется такой вектор
называется такой вектор 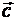 =
=  -
-  , что выполняется равенство
, что выполняется равенство 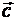 +
+  =
= 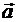 .
.
Легко показать, что для любого вектора  , существует такой единственный вектор
, существует такой единственный вектор  , называемый противоположным вектору
, называемый противоположным вектору 
что  +
+  =
= 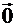 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , будем обозначать –
, будем обозначать –  .
.
Определение. Произведением вектора  на число λ (λ
на число λ (λ 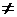 0) называется вектор
0) называется вектор  =λ
=λ  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) векторы  и
и  одинаково направлены, если λ>0, и противоположно направлены, если λ<0;
одинаково направлены, если λ>0, и противоположно направлены, если λ<0;
2) |  |=|λ||
|=|λ||  |.
|.
По определению, произведение произвольного вектора  на число 0 есть нулевой вектор, т.е. 0
на число 0 есть нулевой вектор, т.е. 0  =
= 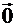 .
.
Введенные операции сложения векторов и умножение вектора на число называются линейными. Они обладают следующими свойствами:
1) сложение векторов коммутативно:
 +
+  =
=  +
+  , "
, "  ,
,  ;
;
2) сложение векторов ассоциативно:
( +
+  )+
)+ 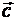 =
=  +(
+( +
+ 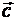 ), "
), "  ,
,  ,
, 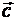 ;
;
3)  +
+ 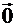 =
=  , "
, "  ;
;
4)  +(-
+(-  )=0, "
)=0, "  ;
;
5) умножение вектора на число ассоциативно:
α (β  ) = (α β)
) = (α β)  , "
, "  " α, β Î R;
" α, β Î R;
6) 1  =
=  , "
, "  ;
;
7) умножение вектора на число дистрибутивно по отношению к
сложению чисел:
(α+β)  =α
=α  +β
+β  , "
, "  , " α, β Î R;
, " α, β Î R;
8) умножение вектора на число дистрибутивно по отношению к сложению векторов:
α( +
+  )=α
)=α  +α
+α  , "
, "  ,
,  , " α Î R;
, " α Î R;
Множество всех векторов пространства (плоскости), удовлетворяющих свойствам 1) – 8), называется линейным, или векторным пространством, и обозначается  (
( ).
).
Теорема (необходимое и достатаочное условие коллинеарности двух векторов). Для того чтобы векторы  и
и  были коллинеарны, необходимо и достаточно, чтобы существовало число λ, удовлетворяющее условию:
были коллинеарны, необходимо и достаточно, чтобы существовало число λ, удовлетворяющее условию:
 = λ
= λ  .
.
Проекции.
Назовем осью прямую, на которой указано направление, которое будем называть положительным.
Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α'||α и обозначим точку пересечения плоскости α' c осью l через А1. Тогда точка А1 называется проекцией точки А на ось l относительно плоскости α. В частности, если α 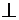 l, то проекция называется прямоугольной, или ортогональной.
l, то проекция называется прямоугольной, или ортогональной.

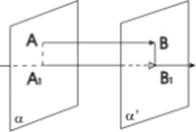
Пусть теперь задан вектор  . Возьмем проекции А1 и В1 точек А и В на ось l относительно плоскости α.
. Возьмем проекции А1 и В1 точек А и В на ось l относительно плоскости α.
Тогда вектор 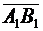 называется проекциейвектора
называется проекциейвектора  на ось l относительно плоскости α. Величиной проекции вектора
на ось l относительно плоскости α. Величиной проекции вектора  на ось l относительно плоскости α называется число, равное:
на ось l относительно плоскости α называется число, равное:
а) | 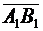 |, если направление вектора
|, если направление вектора 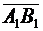 совпадает с направлением оси l;
совпадает с направлением оси l;
б) - | 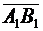 |, если направление
|, если направление 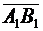 противоположно направлено оси l.
противоположно направлено оси l.
Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора  на ось l будем обозначать Пр l
на ось l будем обозначать Пр l  , а для ортогональной проекции использовать обозначение пр l
, а для ортогональной проекции использовать обозначение пр l  .
.
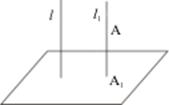 Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l 1 || l и обозначим точку пересечения прямой l 1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l.
Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l 1 || l и обозначим точку пересечения прямой l 1 с плоскостью α через А1. Точка А1 называется проекциейточки А наплоскость α относительнопрямой l.
Если прямая l 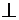 α, то проекция называется прямоугольной, или ортогональной.
α, то проекция называется прямоугольной, или ортогональной.
Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью.
Из определения следует, что 0  α
α  π. Угол между векторами или между осями, или между вектором и осью будем обозначать соответственно: (
π. Угол между векторами или между осями, или между вектором и осью будем обозначать соответственно: (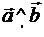 ), (
), (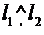 ), (
), ( ).
).
Теорема. Проекция вектора на ось обладает следуицики свойствами:
1)  ;
;
2) 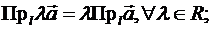
3) 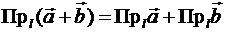 .
.
Не нашли, что искали? Воспользуйтесь поиском: