
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Зависимость урожайности от внесенных удобрений
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Урожайность зерновых (ц/га) | ||||||||||
| Внесено удобрений (кг/га) | 4,0 | 2,5 | 5,0 | 5,8 | 7,5 | 5,7 | 7,0 | 3,0 | 6,0 | 3,5 |
Решение
Решение проведем с использованием ППП MS Excel..
Создадим файл с исходными данными в среде MS Excel. Исходные данные разместим в таблице следующей структуры (рис.5.7):
- Х (Внесено удобрений, кг/га)
- Y (Урожайность зерновых, ц/га)
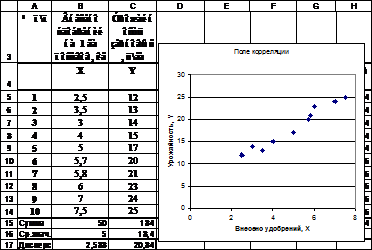
Рис. 5.7. Excel. Исходные данные и поле корреляции.
1. Значения описательных статистик по каждой переменной найдем, используя надстройку Сервис - Пакет анализа - Описательная статистика (Рис. 5.8.).

Рис. 5.8. Excel. Описательные статистики.
Определим коэффициенты вариации переменных:
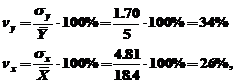
Варьирование признаков находится в допустимом пределе (<35%).
2. Построим поле корреляции моделируемого 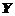 (Урожайность зерновых) и факторного признака
(Урожайность зерновых) и факторного признака 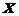 (Внесено удобрений). Для построения используем Мастер диаграмм – тип Точечная.
(Внесено удобрений). Для построения используем Мастер диаграмм – тип Точечная.
Как следует из рис.5.7, с увеличением количества внесенных удобрений на 1 га посевов урожайность зерновых растет примерно линейно. Следовательно, для данной зависимости можно попытаться построить линейное уравнение регрессии.
3. Найдем значение линейного коэффициента корреляции двумя способами:
- непосредственно по определению, формула (5.1);
- используя встроенную функцию КОРЕЛЛ().
В обоих случаях получили значение коэффициента корреляции 0.977, что говорит о наличии существенной линейной корреляции между признаками.
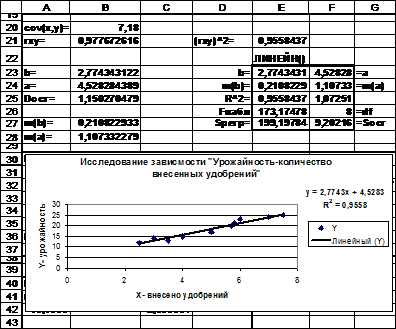
Рис. 5.9. Вычисление коэффициента корреляции и параметров уравнения регрессии в Excel (режим отображения данных).
4. Определим параметры уравнения парной регрессии – коэффициенты линейного уравнения и их ошибки (средние квадратические погрешности) - тремя способами:
- непосредственно по определению (формулы 5.9 и 5.17);
- используя встроенную функцию ЛИНЕЙН();
- используя ЛИНИЮ ТРЕНДА.
Во всех случаях получим уравнение  (рис.5.10), откуда следует, что каждый килограмм внесенного удобрения увеличивает урожайность на 2.77 ц/га. Если удобрения не вносить (Х =0), то урожайность будет равна 4.53 ц/га.
(рис.5.10), откуда следует, что каждый килограмм внесенного удобрения увеличивает урожайность на 2.77 ц/га. Если удобрения не вносить (Х =0), то урожайность будет равна 4.53 ц/га.

Рис 5.10. Вычисление коэффициента корреляции и параметров уравнения регрессии в Excel (режим отображения формул).
5. Вычислим коэффициент детерминации R2. Для этого воспользуемся формулой (5.11). Все вычисления показаны на рис.5.11 и 5.12.
Чтобы найти 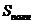 воспользуемся знанием Yср (ячейка С16) и заполним столбец I. Чтобы найти
воспользуемся знанием Yср (ячейка С16) и заполним столбец I. Чтобы найти 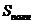 ,
,  и
и  необходимо знать теоретические значения отклика
необходимо знать теоретические значения отклика  (Y теор). Для каждого значения фактора
(Y теор). Для каждого значения фактора 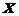 по полученному уравнению регрессии
по полученному уравнению регрессии 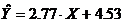 вычислим теоретические значения
вычислим теоретические значения  (столбец J). Найдем остатки - разность между исходными значениями и вычисленными значениями отклика по уравнению регрессии (столбец K). Вычислим сумму квадратов остатков
(столбец J). Найдем остатки - разность между исходными значениями и вычисленными значениями отклика по уравнению регрессии (столбец K). Вычислим сумму квадратов остатков  (столбец L) и
(столбец L) и  (столбец M). Искомое значение коэффициента детерминации R2 вычислено в ячейке H18, оно равно 0.9558. Таким образом, 95.58% вариации Y объясняется вариацией фактора X, или 95,6% вариации урожайности объясняется вариацией количества внесенных удобрений, т.е. сила линейной связи между количеством внесенных удобрений и урожайностью весьма высокая.
(столбец M). Искомое значение коэффициента детерминации R2 вычислено в ячейке H18, оно равно 0.9558. Таким образом, 95.58% вариации Y объясняется вариацией фактора X, или 95,6% вариации урожайности объясняется вариацией количества внесенных удобрений, т.е. сила линейной связи между количеством внесенных удобрений и урожайностью весьма высокая.
Значение R2 для линейной регрессии могло быть получено другим способом - используя соотношение 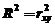 , для проверки вычислим
, для проверки вычислим 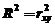 =(0.9776)2=0.9558. Вычисленные R2 значения совпали. Заметим, что в процессе решения значение R2 было вычислено по крайней мере дважды:
=(0.9776)2=0.9558. Вычисленные R2 значения совпали. Заметим, что в процессе решения значение R2 было вычислено по крайней мере дважды:
· при использовании функции ЛИНЕЙН(), ячейка Е25;
· при построении линии тренда.

Рис. 5.11.Вычисление коэффициента детерминированности
Лист Excel в режиме отображения данных.

Рис.5.12. Вычисление коэффициента детерминированности.
Лист MS Excel в режиме отображения формул.
6. Оценим статистическую значимость уравнения в целом, используя критерий Фишера.
Нулевая гипотеза H0: уравнение регрессии не значимо, коэффициент детерминации R2 =0. Альтернативная гипотеза H1: коэффициент детерминации 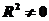 и уравнение в целом значимо.
и уравнение в целом значимо.
 :
:
С помощью функции FРАСПОБР() для уровня значимости 0,05 находим Fкрит. Число степеней свободы для регрессионной суммы равно 1, для остаточной суммы равно 8. Тогда Fкрит = FРАСПОБР(0,05;1;8)=5.31 (рис. 5.13).
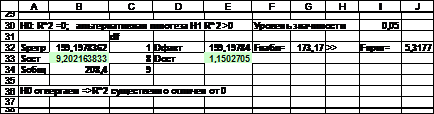
Рис. 5.13. MS Excel. Проверка гипотезы о статистической значимости уравнения регрессии.
Так как 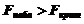 , принимаем альтернативную гипотезу о значимости коэффициента детерминации и всего уравнения в целом.
, принимаем альтернативную гипотезу о значимости коэффициента детерминации и всего уравнения в целом.
6. Оценим статистическую значимость параметров уравнения регрессии.
Значения стандартной ошибки 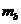 и
и 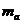 параметров определим пользуясь формулами (5.17), все вычисления реализованы на рис.5.9-5.10, ячейки А27 и А28. В результате получили
параметров определим пользуясь формулами (5.17), все вычисления реализованы на рис.5.9-5.10, ячейки А27 и А28. В результате получили 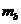 =0.2108 и
=0.2108 и 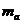 =1.1073. Этот же результат получен как результат работы функции ЛИНЕЙН() вячейках E24 и F24 на тех же рисунках.
=1.1073. Этот же результат получен как результат работы функции ЛИНЕЙН() вячейках E24 и F24 на тех же рисунках.
7. Проведем оценку статистической значимости коэффициента регрессии (b), используя критерий Стьюдента.
Выдвигаем нулевую гипотезу H0:  коэффициент регрессии равен нулю. Альтернативная гипотеза- H1:
коэффициент регрессии равен нулю. Альтернативная гипотеза- H1: 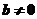 .
.
Вычисляем значение критерия 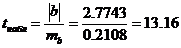 .
.
Находим 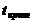 с помощью функции СТЬЮДРАСПОБР(), для уровня значимости 0,05 и числа степеней свободы 8 СТЬЮДРАСПОБР(0,05;8)=2,306.
с помощью функции СТЬЮДРАСПОБР(), для уровня значимости 0,05 и числа степеней свободы 8 СТЬЮДРАСПОБР(0,05;8)=2,306. 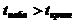 , следовательно, принимаем альтернативную гипотезу, т.е. коэффициент регрессии существенно отличен от нуля.
, следовательно, принимаем альтернативную гипотезу, т.е. коэффициент регрессии существенно отличен от нуля.
Статистическая значимость свободного члена (a), оценивается аналогично. Для этого выдвигаем нулевую гипотезу H0: 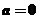 , свободный член равен нулю. Альтернативная гипотеза H1:
, свободный член равен нулю. Альтернативная гипотеза H1:  .
.
Вычисляем значение критерия
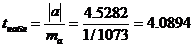 .
.
Найденное выше 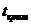 =2,306, сравниваем с
=2,306, сравниваем с 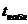 , поскольку
, поскольку 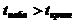 , то принимаем альтернативную гипотезу о значимости свободного члена уравнения регрессии.
, то принимаем альтернативную гипотезу о значимости свободного члена уравнения регрессии.
Так как a, b и 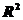 не случайно отличаются от нуля, полученное уравнение линейной регрессии значимо с вероятностью 95%, как и параметры этого уравнения и может быть использовано для анализа и прогноза.
не случайно отличаются от нуля, полученное уравнение линейной регрессии значимо с вероятностью 95%, как и параметры этого уравнения и может быть использовано для анализа и прогноза.
8. Определим доверительные интервалы для b и a по формуле (5.19):
- для коэффициента регрессии b:
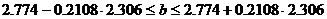

- для свободного члена a:
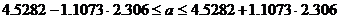
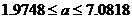
Поскольку с надежностью 95% доверительные интервалы для коэффициентов a и b уравнения регрессии не содержат ноль, то это подтверждает вывод об их статистической значимости.
9. Остатки - разность между исходными и вычисленными по уравнению регрессии значениям уже вычислены., и содержатся в столбце K на рис.5.11 - 5.12.
Вычислим сумму значений остатков. Построим график остатков (рис. 5.14).

Рис. 5.14. График остатков.
Сумма значений остатков равна нулю, следовательно, первое условие Гаусса-Маркова выполняется (равенство нулю математического ожидания случайной компоненты). Из визуального анализа графика можно сделать вывод, что тенденция остатков не прослеживается, т.е. условие гомоскедастичности не нарушается.
10. Построим интервальную оценку прогноза для ожидаемого значения урожайности.
Среднее значение X =5кг/га. Найдем прогноз урожайности при увеличении среднего значения внесенных удобрений на 5%, то есть для  .
.

Рис. 5.15. Вычисление интервальной оценки прогноза в Excel (режим отображения данных).
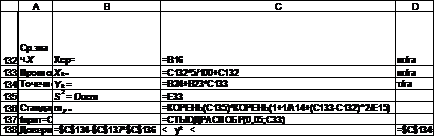
Рис. 5.16. Вычисление интервальной оценки прогноза в Excel (режим отображения формул).
Точечный прогноз получим подстановкой значения X в уравнение регрессии:  ц/га. Предельная ошибка прогноза, которая в 95% случаев не будет превышена, вычисляется по соотношению (5.21) и составляет 1,126 ц/га. Таким образом, интервальная оценка прогноза составит
ц/га. Предельная ошибка прогноза, которая в 95% случаев не будет превышена, вычисляется по соотношению (5.21) и составляет 1,126 ц/га. Таким образом, интервальная оценка прогноза составит
16,49 ц/га < Y < 21,69 ц/га
Таким образом, при увеличении среднего значения внесенных удобрений на 5%, значение урожайности с вероятностью 95% окажется в интервале 16,49 ц/га < Y < 21,69 ц/га
11. Вычислим коэффициенты регрессии матричным методом (используя формулу 5.28). Все расчеты приведены на рис.5.17-5.18.
 Рис. 5.17. Вычисление коэффициентов регрессии матричным методом в MS Excel (режим отображения данных).
Рис. 5.17. Вычисление коэффициентов регрессии матричным методом в MS Excel (режим отображения данных).
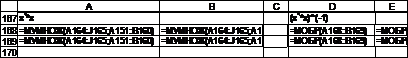
Рис. 5.18. Вычисление коэффициентов регрессии матричным методом в MS Excel (режим отображения формул - начало).

Рис. 5.19. Вычисление коэффициентов регрессии матричным методом в Excel (режим отображения формул - конец).
11. Вычисление характеристик линейного уравнения регрессии с использованием средства «Регрессия» надстройки «Пакет анализа» MS Excel, приведено на рис.5.5-5.6/
Все характеристики совпадают со значениями вычисленными вручную (по определению).
Не нашли, что искали? Воспользуйтесь поиском: