Теоретические сведения. В уравнении (5.3) функция может быть и нелинейной

В уравнении (5.3) функция может быть и нелинейной. Выбор вида функции может быть осуществлен путем анализа поля корреляции. По форме облака рассеяния выбирают функцию, имеющую подходящий график (рис.6.1.).

Рис.6.1 Основные типы кривых, используемые при количественной оценке связей между двумя переменными.

Выделяют два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например, полиномы разных степеней – или гипербола – ;

2. Регрессии, нелинейные по оцениваемым параметрам, например, степенная функция - , или показательная функция - .

В первом случае МНК применяется так же, как и в линейной регрессии, а система нормальных уравнений для определения коэффициентов будет линейной, которую можно решить любым известным способом. В случае квадратичной зависимости

(6.1)

система нормальных уравнений для определения коэффициентов примет вид:

(6.2)

Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия , то в моделях, нелинейных по оцениваемым параметрам, процедура МНК применяется не к исходным данным, а к их преобразованным величинам. Вследствие этого оценки параметров регрессии для линеаризуемых функций МНК оказываются несколько смещенными.

Рассмотрим уравнение нелинейное относительно включенной объясняющей переменой , но линейное по параметрам .

Произведем замену , тогда уравнение примет линейную форму уравнения множественной регрессии:

(6.3)

Для равносторонней гиперболы переход к линейной зависимости осуществляется путем введения новой независимой переменной, равной .

В случае, если нелинейная модель внутренне линейна, то путем соответствующих преобразований она может быть приведена к линейному виду.

Для каждой из этих зависимостей это преобразование может быть своё. Для степенной, экспоненциальной и показательной зависимостей это достигается путем логарифмирования,

Рассмотрим линеаризацию на примере экспоненциальной зависимости

(6.4)

Линеаризация достигается путем логарифмирования равенства (6.4), после чего получаем соотношение

(6.5)

Обозначим и соответственно через и , тогда зависимость (6.4) может быть записана в виде , что позволяет применить формулы для вычисления коэффициентов линейной зависимости (с заменой на и на ).

Линеаризующие преобразования для различных видов функций приведены в табл.6.1.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция . Параметр b в степенной зависимости имеет четкое экономическое истолкование, он является коэффициентом эластичности.

Таблица 6.1

Исходная функция	Замена	Линейное уравнение
квадратичная
экспоненциальная
показательная
степенная
равносторонняя гипербола

Коэффициент эластичности, определяемый соотношением (5.24), показывает, насколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Формулы для вычисления коэффициента для различных видов функций приведены в таблице 6.2.

Очевидно, что все коэффициенты эластичности, кроме коэффициента эластичности для степенной функции, не являются постоянными и зависят от Х. Поэтому для характеристики эластичности используют так называемый средний коэффициент эластичности 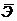– т.е. коэффициент эластичности, вычисленный в точке :

Таблица 6.2

Исходная функция, Y	Первая производная,	Коэффициент эластичности, Э
линейная
квадратичная
степенная
показательная
равносторонняя гипербола

Не нашли, что искали? Воспользуйтесь поиском: