
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Прямоугольные аксонометрические проекции
4.2.1. Прямоугольная изометрическая проекция. В данной проекции k = m = n = 0,82. Для упрощения построений принимают k = m = n = 1, то есть масштаб при откладывании координат по всем трём аксонометрическим осям равен 1:1. Расположение аксонометрических осей показано на рис. 4.2.
 С целью упрощения на этом и последующих рисунках подстрочный индекс «А» при обозначении аксонометрических проекций геометрических объектов (точек, прямых, осей координат) опущен. Такое упрощение применяется и в другой литературе, в том числе в учебном пособии «Рабочая тетрадь по техническому рисунку в аксонометрии», которое используется при проведении практических занятий по дисциплине «Технический рисунок».
С целью упрощения на этом и последующих рисунках подстрочный индекс «А» при обозначении аксонометрических проекций геометрических объектов (точек, прямых, осей координат) опущен. Такое упрощение применяется и в другой литературе, в том числе в учебном пособии «Рабочая тетрадь по техническому рисунку в аксонометрии», которое используется при проведении практических занятий по дисциплине «Технический рисунок».
Для построения в прямоугольной изометрии аксонометрической проекции точки В по её координатам xВ, yВ, zB (рис. 4.1) вдоль оси Oх (рис. 4.2) откладываем отрезок, равный xВ. Из полученной точки ВХ параллельно оси Oy проводим отрезок длиной yВ и получаем точку В1. Точка В1 (на рис. 4.1 ей соответствует точка В1А)называется вторичной проекцией точки В. Далее, проведя через точку В1 отрезок, равный zВ параллельно оси Oz, получим аксонометрическую проекцию точки В. Ломаная линия OВХВ1В называется трёхзвенной координатной линией.
Для построения аксонометрической проекции отрезка прямой необходимо построить проекции двух точек концов отрезка с помощью трёхзвенной координатной линии и соединить построенные точки прямой линией.
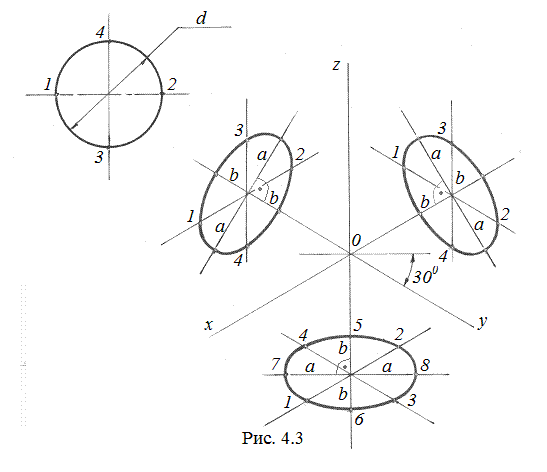
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 4.3), причём малая ось эллипса совпадает с направлением оси координатной системы, отсутствующей в данной плоскости.
Так, если окружность расположена в плоскости хOy, то малая ось эллипса параллельна оси Oz, а большая перпендикулярна ей. При k = m = n = 1 большая ось 2 a= 1,22 d, малая ось 2 b = 0,71 d, где d – диаметр окружности.
На рис. 4.3 эллипсы построены по восьми точкам.
На рис. 4.4 показано построение эллипса по большой оси AB (2 a = 1,22 d) и малой оси CD (2 b = 0,71 d). Из точки O проведены две концентрические окружности. Большую из них делят на несколько частей. Через точки деления и центр O проводят радиусы, которые делят также вторую окружность.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

4.2.2. Прямоугольная диметрическая проекция. Коэффициенты искажения: k = n = 0,94 и m = 0,47. Для упрощения построения коэффициенты принимают равными k = n = 1 и m = 0,5, то есть масштаб по осям х и z равен 1:1, а по оси y равен 1:2.
На рис. 4.5 показано положение аксонометрических осей: угол наклона оси Oх к горизонтальной линии равен 7°10', угол наклона оси Oy к горизонтальной линии равен 41°25'.
На рис. 4.5 показаны также направления малой и большой осей эллипса (м.о. и б.о.) в трёх координатных плоскостях и величины большой и малой осей. Эллипсы можно построить по восьми точкам.

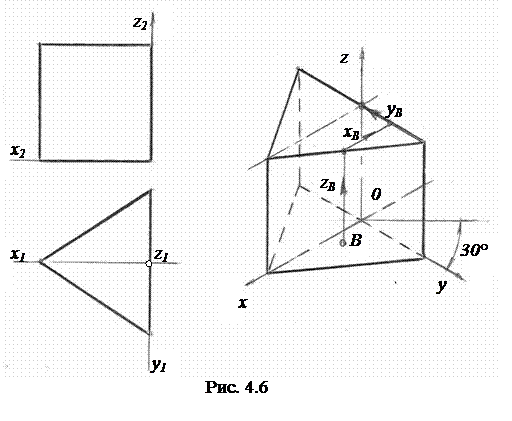
4.2.3. Пространственные геометрические объекты в прямоугольной аксонометрии. На рис. 4.6 по ортогональным проекциям призмы построена её изометрическая проекция.
На видимой грани призмы задана точка B, и выполнена задача, обратная показанной на рис. 4.2 – определены координаты точки В (xВ, yВ, zВ) относительно точки O с помощью трёхзвенной координатной линии.
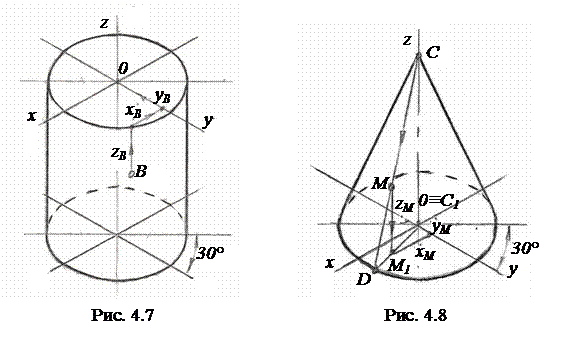
На рис. 4.7 изображён в прямоугольной изометрии цилиндр, верхнее основание которого расположено в плоскости xOy. На видимой части поверхности цилиндра задана точка B и определены её координаты xВ, yВ, zВ относительно точки O с помощью трёхзвенной координатной линии.
На рис. 4.8 изображён в прямоугольной изометрии конус, стоящий основанием на плоскости xOy. На видимой части поверхности конуса задана точка M. Для определения её координат xМ, yМ, zМ относительно точки O через точку M проведена образующая CD.
 .
.
Не нашли, что искали? Воспользуйтесь поиском: