Тени от точки, прямой и плоской фигуры.

Тень от точки будет там, где луч света, проходящий через точку, пересечёт поверхность, на которую падает тень. Пусть точка A задана двумя ортогональными проекциями A₁ и A₂, а направление светового луча задано его аксонометрической проекцией r и вторичной проекцией r₁ (рис. 5.3).

Для построения аксонометрии тени от точки A на плоскость хOy построим изометрическую проекцию точки по трём координатам х_А, y_А, z_А. Затем через точку A проводим луч параллельно проекции r светового луча, а через её вторичную проекцию A₁ проводим прямую параллельно вторичной проекции луча r₁. Пересечение этих двух прямых и определяет аксонометрию тени A₀ от точки A на плоскость хOy

.

На рис. 5.4 показано построение аксонометрии тени от точки A на горизонтально-проецирующую плоскость BCDE. Для этого через точку A проведена вспомогательная горизонтально-проецирующая плоскость Σ (A₁1| | r₁ , A2| | r₁). Определяется линия пересечения 1-2 =BCDE 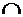Σ.

Проведя через точку A луч параллельно r, на линии 1-2 получим аксонометрию тени A ₀ от точки A на плоскости BCDE.

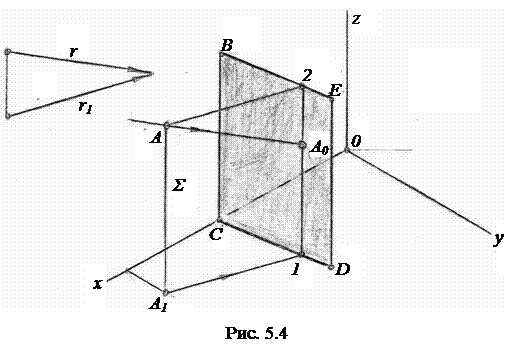
На рис. 5.5 приведено построение тени от прямой общего положения AB и от горизонтально-проецирующей прямой CD на плоскость хOy в прямоугольной изометрии при заданных направлениях r и r₁. Падающие тени от прямых AB и CD строим по двум точкам, принадлежащим каждой из них.

Из точек A, B, C, D проводим лучи, параллельные r, а из точек A₁, B₁, C₁, D₁ проводим лучи, параллельные r₁. В результате пересечения пар соответствующих прямых находим тени A₀B₀ и C₀D₀ от прямых AB и CD. При этом тень C₀D₀ совпадает по направлению с вторичной проекцией r₁ луча r.

Отметим некоторые свойства теней прямых:

1) Тень отрезка прямой равна и параллельна самому отрезку, когда прямая параллельна плоскости, на которую она отбрасывает тень.

2) Параллельные прямые имеют параллельные тени.

3) Прямая будет иметь тень в виде точки, если её направление совпадает с направлением светового луча.

4) Если отрезок перпендикулярен плоскости проекций, его тень на этой плоскости будет совпадать с одноимённой проекцией светового луча.

Построение тени от многоугольника сводится к построению тени от всех его сторон. На рис. 5.6 дано построение тени от непрозрачного треугольника ABC на плоскость хOy в изометрии при заданных r и r₁.

Если плоскость фигуры расположена параллельно световым лучам, то её тенью будет прямая линия.

Тень от плоской фигуры на параллельную ей плоскость равна этой фигуре.

Не нашли, что искали? Воспользуйтесь поиском: