Произвольный четырехугольник

Площадь выпуклого четырехугольника определяется по формуле , где и - диагонали четырехугольника, - угол между диагоналями.

Для того чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы сумма длин противоположных сторон были равны друг другу.

Для того чтобы вокруг выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны .

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны. У параллелограмма равны противолежащие стороны и углы. Для того, чтобы выпуклый четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали в точке пересечения делились пополам.

Точка пересечения диагоналей параллелограмма является центром симметрии параллелограмма.

Около параллелограмма можно описать окружность в том и только в том случае, если он является прямоугольником.

В параллелограмм можно вписать окружность в том и только в том случае, если он является ромбом.

Пусть , - длины смежных сторон параллелограмма, - величина угла между этими сторонами, - высота, опущенная на сторону , и - дины диагоналей. Справедливы следующие соотношения.

,

,

,

,

.

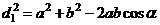Прямоугольник

Если один из углов параллелограмма – прямой, то и все остальные углы – прямые. Такой параллелограмм называется прямоугольником. Диагонали прямоугольника равны. Площадь прямоугольника определяется по формуле .

Ромб

Если в параллелограмме все стороны равны, но называется ромбом. Диагонали ромба взаимно перпендикулярны и делят углы ромба пополам. Площадь ромба равняется .

Квадрат

Квадратом называется параллелограмм с равными сторонами и прямыми углами. Квадрат является частным случаем прямоугольника (это прямоугольник с равными сторонами) и ромба (это ромб с прямыми углами). Поэтому квадрат обладает всеми свойствами прямоугольника и ромба. Площадь квадрата равняется .

Трапеция

Трапеция – это выпуклый четырехугольник, у которого две противоположные стороны (основания) параллельны, а две другие непараллельны.

Средней линией трапеции называется отрезок прямой, соединяющей середины непараллельных (боковых) сторон трапеции. Средняя линия трапеции параллельна ее основанию. Длина средней линии равна полусумме длин ее оснований .

Около трапеции можно описать окружность в том и только в том случае, если она равнобокая, т.е. если ее боковые стороны равны.

Высота равнобокой трапеции, в которую можно вписать окружность, является средним геометрическим ее оснований, т.е. .

Отрезок, параллельный основанию, и делящий трапецию на две равновеликие трапеции равен .

Отрезок, параллельный основанию, и делящий трапецию на две подобные трапеции равен .

Отрезок, параллельный основанию, и проходящий через точку пересечения диагоналей равен .

Площадь трапеции определяется по формуле ,

где , - длины оснований трапеции, - ее высота, - длина средней линии.

Площадь равнобедренной трапеции, диагонали которой перпендикулярны, равна квадрату ее высоты, т.е. .

Окружность и круг

Пусть - длина радиуса некоторого круга, - длина окружности этого круга и - его площадь. Тогда , .

Угол между двумя радиусами окружности называется центральным углом. Если - радианная мера центрального угла, то длина дуги окружности равна ,

площадь центрального сектора равна ,

площадь сегмента равна .

Угол, образованный двумя хордами, исходящими из одной точки окружности, называется вписанным углом. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу окружности. Следствие: углы, опирающиеся на диаметр – прямые. Вписанные углы, опирающиеся на одну и ту же длину окружности, равны между собой.

Касательные, проведенные к окружности из одной ее точки, имеют одинаковую длину, а центр окружности находиться на биссектрисе угла, образованного этими касательными. Радиус, проведенный в точку касания, перпендикулярен касательной.

Если хорды и окружности пересекаются в точке , то .

Если из точки к окружности проведены две секущие, пересекающие ее в точках , и , соответственно, то .

Радиус окружности, описанной вокруг правильного многоугольника ( - количество сторон многоугольника, - длина стороны), определяется формулой:

, описанной вокруг правильного многоугольника: .

Многоугольники

Длина ломанной не меньше отрезка соединяющего ее концы.

Сумма внутренних углов выпуклого -угольника равна . Сумма внешних углов выпуклого -угольника, взятых по одному при каждой вершине, равна .

Правильный выпуклый многоугольник является вписанным в окружности и описанным вокруг окружности. Правильные выпуклые -угольники подобны. В частности, если у них стороны равны, то они равны. Следствие: у правильных -угольников отношения периметров, радиусов вписанных и описанных окружностей равны.

Не нашли, что искали? Воспользуйтесь поиском: