Площадь треугольника

Для нахождения площади треугольника самой важной является формула , где h_a – высота треугольника, опущенная на сторону а. Важность этой формулы заключается в том, что в отличии от многих других по этой формуле можно найти площадь треугольника, имея информацию только о двух его компонентах (стороне и высоте). Из этой формулы, в частности, следует, что площадь прямоугольного треугольника равна половине произведения его катетов. Зная две стороны а и b треугольника, а также угол a между ними, площадь находится по формуле . Если же известны все три стороны а, b и с, то по формуле Герона имеем , где р – полупериметр треугольника. Полезными могут оказаться также формулы и не встречающиеся в школьном учебнике:

, где a и b - углы треугольника, прилежащие к его стороне а и также

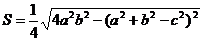– аналог формулы Герона (известны все три стороны). Можно переходить к решению заданий 3.1 – 3.5.

3.1. Найдите площадь треугольника со сторонами и 4.

3.2. Найдите площадь треугольника, две стороны которого равны 4 и 5, а косинус угла между ними равен 0,6.

3.3. Найдите площадь тупоугольного равнобедренного треугольника, у которого две высоты равны 15 и 24.

3.4. Найдите площадь треугольника АВС, у которого АС = 4 и для некоторой точки D, лежащей на стороне АС, выполняются условия: BD = 5 и CosÐBDC = 0,8.

3.5. Найдите площадь треугольника АВС, у которого АВ = 13, ВС = 15 и tgÐC = 4/3.

Не нашли, что искали? Воспользуйтесь поиском: