Многоугольники и их компоненты

Многоугольником или точнее n-угольником называют часть плоскости, ограниченную n-звенной (n ³ 3) замкнутой ломаной без самопересечений. Вершины и звенья этой ломаной соответственно называют вершинами и сторонами этого многоугольника. На рисунке 12 (слева – направо) изображены выпуклый и невыпуклый четырехугольники. Под выпуклым многоугольником понимают такой, который расположен в одной полуплоскости относительно каждой прямой, проходящей через его стороны. Многоугольник является выпуклым тогда и только тогда, когда

все его внутренние углы меньше 180⁰.

Сумма всех внутренних углов любого

(и даже невыпуклого) n-угольника равна

(n – 2)×180 ⁰. Отрезок, соединяющий не смеж-

ные (не лежащие на одной стороне) вершины Рис. 12

называется диагональю многоугольника. В n-угольнике n(n – 3)/2 диагоналей. Если d₁, d₂ – длины диагоналей четырехугольника, угол между которыми равен a, то площадь этого четырехугольника может быть найдена по формуле . Оказывается, что в четырехугольнике, с перпендикулярными диагоналями, суммы квадратов противоположных сторон равны.

Окружность, проходящая через все вершины многоугольника, называют описанной около него, а окружность, касающуюся каждой его стороны, – вписанной в этот многоугольник. Ясно, что если около многоугольника описана окружность или в него вписана окружность, то он является обязательно выпуклым. Не во всякий даже выпуклый многоугольник можно вписать окружность, но если ее можно в него вписать, то она единственна и ее радиус может быть найден по формуле r = S/p, где S – площадь и p – полупериметр этого многоугольника. Также не около всякого многоугольника можно описать окружность. Если около некоторого многоугольника все же можно описать окружность, то она единственна и его обычно называют вписанным, а радиус этой окружности, зная информацию о двух каких-то смежных сторонах и углу между ними, можно найти как радиус окружности, описанной около треугольника, построенного на этих двух смежных сторонах многоугольника. Полезно знать связанные с описанной и вписанной окружностями четырехугольника следующие два утверждения:

- около четырехугольника можно описать окружность тогда и только тогда, когда сумма его двух каких-то противоположных углов равна 180⁰;

- в четырехугольник можно вписать окружность тогда и только тогда, когда он выпуклый и суммы его противоположных сторон равны.

Многоугольник, у которого все стороны равны и все внутренние углы тоже равны, называется правильным. В такой многоугольник можно вписать окружность, а также около него можно описать окружность, причем центры этих окружностей совпадают. Необходимые формулы, связанные с правильным n-угольником A₁A₂…A_n, можно получить в результате рассмотрения треугольника А₁ О А₂, где О – центр вписанной (а значит и описанной) окружности. Действительно, угол А₁ О А₂ равен 360⁰ / n (кстати, внешний угол при вершине правильного n-угольника тоже равен 360⁰ / n), А₁ О – радиус описанной около многоугольника окружности, высота треугольника А₁ О А₂, проведенная из О, – радиус вписанной в многоугольник окружности, – площадь n-угольника и т. д.. Для примера приведем одну из версий таких формул для правильного n-угольника, в случае, когда известна длина а его стороны:

где a, r, R и S - соответственно внутренний угол, радиус вписанной окружности, радиус описанной окружности и площадь этого правильного n-угольника.

Теперь можно переходить к решению заданий 3.1 – 3.5.

8.1. В пятиугольник с площадью 22 вписали окружность радиуса 2. Найдите наименьшую из его сторон, если их длины относятся как 3: 2: 1: 2: 3.

8.2. В правильном шестиугольнике А₁ А₂…А₆ проекция диагонали А₁ А₃ на диагональ А₃ А₆ равна . Найдите площадь вписанного в этот шестиугольник круга.

8.3. Около правильного многоугольника А₁ А₂ …А_n с внешним углом 30 ⁰ описана окружность радиуса . Найдите расстояние от точки А₁ до прямой А₃ А₈.

8.4. Найдите диаметр окружности, описанной около четырехугольника со сторонами 7, 15, 20 и 24.

8.5. В четырехугольник с перпендикулярными диагоналями вписана окружность. Найдите ее радиус, если известно, что какие-то две стороны четырехугольника равны 13 и 15, а одна из его диагоналей равна 24.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны. Условие о том, что четырехугольник является параллелограммом, равносильно каждому из следующих пяти условий:

- противоположные стороны четырехугольника попарно равны;

- две противоположные стороны четырехугольника равны и параллельны;

- противоположные углы четырехугольника попарно равны;

- точка пересечения диагоналей четырехугольника делит каждую из них пополам;

- каждая из диагоналей четырехугольника делит его на равновеликие треугольники. На рис. 13 изображен параллелограмм ABCD с C B

высотой ВЕ и диагоналями АС и ВD. Его площадь

S может быть найдена по следующим формулам: F

S = AD×BE = AB×AD×SinÐBAD = 0,5×AC×BD×SinÐAFB. D E A

Также выполняется равенство AC ²+BD ²= 2(AB ²+AD ²). Рис. 13

Прямоугольник, ромб и квадрат являются разновидностями параллелограммов. Надо знать, что около параллелограмма можно описать окружность тогда и только тогда, когда он прямоугольник, причем диаметр окружности будет равен диагонали этого прямоугольника. В параллелограмм можно вписать окружность тогда и только тогда, когда он ромб, причем диаметр окружности будет равен высоте этого ромба.

Можно переходить к решению заданий 4.1 – 4.5.

9.1. Окружность, проходящая через вершину А квадрата АВСD, касается его сторон BC и CD соответственно в точках E и F. Найдите радиус этой окружности, если площадь треугольника AEF равна .

9.2. В прямоугольнике АВСD точка Е лежит на диагонали АС. Найдите отношение площадей треугольников ABE и ADE.

9.3. Найдите в градусах тупой угол между диагоналями параллелограмма с площадью , около которого можно описать окружность радиуса 1.

9.4. В параллелограмм с одним из углов, равным 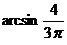, вписан круг. Найдите отношение площадей параллелограмма и круга.

9.5. Биссектриса острого угла А параллелограмма АВСD пересекает прямые BC и CD в двух точках E и F соответственно. Найдите отношение большей высоты параллелограмма и меньшей, если AE / EF = 3.

Трапеция

Трапецией называют четырехугольник, у которого две стороны параллельны, а другие две нет. Ясно, что трапеция – выпуклый четырехугольник. На рис. 14 изображена трапеция АВCD, у которой BC и АD – основания, B C

АB и CD – боковые стороны, EF – средняя ли-

ния, BG – высота и Н – точка пересечения диа- E H F

гоналей. Для решения задач по этой теме нам

могут понадобится следующие сведения:

- EF || AD, EF || BC и ; А G D

- Ð AHB; Рис. 14

- S_ABC = S_BCD, S_ABD = S_ACD, S_AHB = S_CHD;

- D AHD ~ D CHB;

- для равнобедренной трапеции (при АВ = СD) имеем EF = GD и AG = ;

- около трапеции можно описать окружность тогда и только тогда, когда она является равнобедренной;

- если в трапецию можно вписать окружность, то сумма ее оснований равна сумме боковых сторон и поэтому , а значит в равнобедренной трапеции EF = АВ.

Можно переходить к решению заданий 5.1 – 5.5.

10.1. Найдите радиус окружности, вписанной в равнобедренную трапецию с углом 30⁰ и площадью 8.

10.2. Около равнобедренной трапеции ABCD с основаниями AD = 63 и BC = 33 описана окружность. Найдите диаметр этой окружности, если АВ = 39.

10.3. Диагонали трапеции равны 17 и 25, а высота – 15. Найдите площадь трапеции.

10.4. Найдите меньшее основание трапеции, в которую вписана окружность с диаметром 15 и боковые стороны которой равны 17 и 25.

10.5. Найдите высоту трапеции, у которой стороны равны 3; 4; 5 и 1.

Не нашли, что искали? Воспользуйтесь поиском: