Вписанная и описанная окружности треугольника

Во всякий треугольник можно вписать и притом только одну окружность (то есть окружность, касающуюся всех трех его сторон), причем ее центр, как было замечено ранее, совпадает с точкой пересечения биссектрис внутренних углов треугольника. Радиус r вписанной окружности в треугольник с площадью S и полупериметром р можно найти по формуле r = S / p (кстати, зная полупериметр и радиус вписанной окружности, можно также найти площадь треугольника). Это основная формула для нахождения радиуса вписанной окружности не только в треугольник, но и в любой многоугольник, в который окружность можно вписать.

Известно, что около любого треугольника можно описать и притом единственную окружность (то есть окружность, проходящую через все три его вершины), причем ее центр совпадает с точкой пересечений серединных перпендикуляров к сторонам треугольника. Для нахождения радиуса R описанной окружности желательно знать следующие две формулы: R = и , где S – площадь треугольника, a, b и c – его стороны, a - угол против стороны а. Отметим, что вторая формула в отличие от первой позволяет найти радиус описанной окружности по двум компонентам (по стороне и по синусу противолежащего угла) и поэтому является более важной. Реже применяемой, но, тем не менее, полезной является формула S = 2 R² Sina Sinb Sing, связывающая этот радиус с площадью и тремя углами треугольника.

В заключении отметим, что некоторые формулы, на первый взгляд легко выводимые из рассмотренных выше, в случае правильного (равностороннего) или прямоугольного треугольника все же желательно выучить наизусть. К таким формулам относятся:

для правильного треугольника со стороной а; для прямоугольного треугольника с катетами а, b и гипотенузой с.

Можно переходить к решению заданий 5.1 – 5.5.

5.1. Около равностороннего треугольника описана окружность радиуса . Точка D лежит на стороне АС и делит ее в отношении 1: 3, считая от вершины А. Найдите длину отрезка BD.

5.2. Медиана, проведенная из вершины прямого угла треугольника, равна 3, а радиус вписанной в него окружности равен 1. Найдите периметр этого треугольника.

5.3. В равнобедренный треугольник АВС с основанием АС вписана окружность радиуса , пересекающая высоту BD в точке Е. Точка Е делит отрезок BD в отношении 3: 4, считая от конца В. Найдите полупериметр треугольника АВС.

5.4. Найдите площадь равнобедренного треугольника с углом при основании в 15⁰, если радиус описанной около него окружности равен .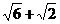

5.5. Найдите радиус окружности, вписанной в треугольник АВС, у которого высота, проведенная из вершины В, равна 15, а также известно, что SinÐA = 3/5 и SinÐC = 15/17.

6. Окружность и ее компоненты

На рис.1 изображен центральный угол АОС, опираю-

ющийся на дугу АВС. Если Ð АОС равен a (радиан) или т⁰,

то говорят, что дуга АВС тоже имеет угловую величину a О

или соответственно т⁰ (напоминаем, что угол в 180⁰ равен

углу в p радиан). Длина окружности радиуса R равна 2pR. a

Если АО = R, тодлина l дуги АВС можетбыть найдена (т⁰)

по формуле l = R a = p R m /180. Площадь круга радиуса А С

R равна p R². Часть круга, ограниченную лучами ОА, ОС

и дугой АВС, называют сектором, опирающимся на дугу В

АВС. Его площадь S находится по формуле S = R² a / 2 Рис. 1 или S = p R² m / 360. Часть сектора, ограниченная хордой АС и дугой АВС, называется сегментом. Его площадь равна разности площадей сектора и треугольника АОС. Известно, что отношение угловых величин дуг одной окружности равно отношению их длин, а также равно отношению площадей секторов, опирающихся на эти дуги.

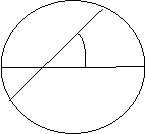На рис. 2 изображен вписанный угол АВС, опирающийся на дугу ADC, а на рис. 3 – угол EFG между касательной FE к окружности и хордой FG, отсекающей дугу FHG. Оказывается, что величины углов АВС и EFG равны половинам угловых величин дуг ADC и FHG соответственно. A

В

М H

G

B E D P

N

A C L

H R

D C G K F

Рис. 2 E F Рис.4

Рис. 3 Рис. 5

Для решения задач по данной теме полезно уметь находить углы между хордами и между секущими окружности. Так, на рис. 4 угол АЕD между хордами АС и BD оказывается равным половине суммы угловых величин дуг AMD и BNC, а на рис. 5 угол FGH между секущими GF и GH равен половине разности угловых величин дуг FPH и KRL.

Приведенные сведения могут быть использованы при решении заданий 1.1 – 1.5.

6.1. Четырехугольник ABCD вписан в окружность радиуса 12/p, причем Ð ВАС = p/8

и Ð DBС = p/6. Найдите длину дуги BCD.

6.2. Точки А и В лежат на разных дугах, стягиваемых хордой CD окружности радиуса . Найдите площадь сегмента, ограниченного хордой АС и меньшей из стягиваемых ею дуг, если Ð ACD = 10⁰ иÐ CBD = 25⁰.

6.3. Четырехугольник ABCD вписан в окружность с центром О, причем Ð ВАD = 50⁰

и Ð ВDС = 10⁰. Найдите угол COD.

6.4. Найдите острый угол между диагоналями четырехугольника ABCD, вписанного в окружность, если Ð АСB = 75⁰ и Ð CAD = 70⁰.

6.5. Окружность проходит через вершины А и В треугольника АВС и пересекает стороны АС и ВС соответственно в точках D и E. Касательная к окружности в точке А образует со стороной АВ угол 75⁰ и Ð АСВ = 45⁰. Найдите угловую величину дуги DE, расположенной внутри треугольника АВС.

Не нашли, что искали? Воспользуйтесь поиском: