Объем наклонного параллелепипеда

Найдем объем наклонного параллелепипеда .

Проведем через ребро плоскость, перпендикулярную основанию 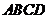, и дополним наклонный параллелепипед треугольной призмой . Теперь отсечем плоскостью, проходящей через ребро перпендикулярно основанию призмы 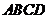, от полученного тела треугольную призму . Получим новый параллелепипед , объем которого равен объему исходного параллелепипеда , т.к. призмы и равны. При описанном преобразовании сохраняются также площадь его основания и высота. При этом плоскости двух граней сохраняются, а плоскости двух других становятся перпендикулярны основаниям.

Применяя еще раз подобное преобразование к наклонным граням, получим прямой параллелепипед. Полученный прямой параллелепипед аналогичным преобразованием превратим в прямоугольный, дополнив его сначала призмой 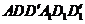, а затем удалив призму 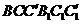. Это преобразование также сохраняет объем параллелепипеда, площадь основания и высоту.

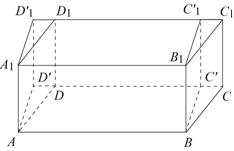
Объем прямоугольного параллелепипеда равен произведению всех трех его измерений, или что то же самое, произведению площади основания на высоту. Поскольку все вышеописанные преобразования сохраняли объем параллелепипеда, площадь основания и высоту, значит объем наклонного параллелепипеда также равен произведению площади основания на высоту.

Объем призмы

Рассмотрим сначала треугольную призму. Дополним ее до параллелепипеда такой же призмой. Объем получившегося параллелепипеда будет вдвое больше объема призмы и равен произведению площади основания на высоту. У призмы и параллелепипеда высоты одинаковые, а площадь основания параллелепипеда вдвое больше площади основания призмы. Следовательно, объем исходной призмы равен произведению площади основания на высоту.

Рассмотрим теперь произвольную призму. Разобьем ее основания на 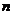треугольников, а исходную призму – на треугольные призмы с боковыми ребрами, параллельными ребрам исходной призмы. При этом объем произвольной призмы будет равен сумме объемов треугольных призм, площадь ее основания будет равна сумме площадей треугольника, а высоты у всех призм будут одинаковы. Таким образом, объем произвольной призмы равен:

.

Таким образом, объем любой призмы равен произведению площади ее основания на высоту.

Объем пирамиды

Теорема 17.1. Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.

Пусть – треугольная пирамида. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма будет состоять из исходной пирамиды и двух равновеликих ей треугольных пирамид и .

Докажем, что эти две пирамиды равновелики исходной. Действительно, у второй и третей пирамид равные основания – и 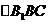и общая высота, проведенная из вершины 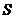. У первой и третей пирамид тоже равны основания – и и общая высота, проведенная из вершины .

Таким образом, все три пирамиды имеют равный объем, значит

.

Рассмотрим теперь произвольную пирамиду. Разобьем ее на 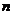треугольных пирамид с общей вершиной и треугольниками в основании, составляющими основание исходной пирамиды. Все треугольные пирамиды будут иметь одинаковую высоту, равную высоте исходной пирамиды. Объем исходной пирамиды равен сумме объемов треугольных пирамид:

.

Таким образом, объем произвольной пирамиды равняется одной трети произведения площади ее основания на высоту.

Не нашли, что искали? Воспользуйтесь поиском: