ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сечение тел вращения
Сечением цилиндра или конуса плоскостью, параллельной плоскости основания, является окружность равная (для цилиндра) или подобная (для конуса) основанию.
Сечением цилиндра плоскостями, параллельными образующим являются прямоугольники. Сечением плоскостями, проходящими через вершину конуса, являются треугольники.
Осевым называется сечение, проходящее через ось тела вращения. Осевое сечение шара (сферы) также называется диаметральным.
Всякое сечение шара плоскостью есть круг. Цент этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Линия пересечения двух сфер есть окружность. Других точек пересечения они не имеют.
Сечением цилиндра или конуса плоскостью, не параллельной плоскости основания и не проходящей через вершину конуса является либо эллипс (если плоскость не пересекает основание), либо парабола и прямая (если плоскость пересекает основание).
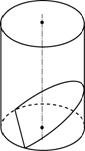
Задачи
21.1Высота цилиндра 6, радиус основания 5. Найти площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 от нее.
21.2В равностороннем конусе (в осевом сечении правильный треугольник) радиус основания 
. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 
.
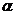21.3Высота конуса 20, радиус его основания 25. Найти площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12.
21.4Радиус основания конуса , образующая наклонена к плоскости основания под углом 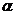. Через вершину конуса проведена плоскость под углом 
к его высоте. Найти площадь получившегося сечения.
21.5Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга.
21.6Радиус шара . Через конец радиуса проведена плоскость под углом 60о к нему. Найти площадь получившегося сечения.
21.7Два равных шара радиуса расположены так, что центр одного из них лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности.
21.8Радиусы шаров равны 25 и 29, а расстояние между их центрами 39. найти длину линии, по которой пересекаются их поверхности.
Не нашли, что искали? Воспользуйтесь поиском: