Свойства вписанных тел

1. Для того чтобы около пирамиды можно было описать шар, необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

2. Для того чтобы около призмы можно было описать шар, необходимо и достаточно, чтобы призма была прямой, и чтобы около ее основания можно было описать окружность.

3. Центр шара, описанного около пирамиды, лежит на перпендикуляре к плоскости основания, проведенном через центр окружности, описанной около основания.

4. Центр шара, описанного около призмы, является серединой отрезка, соединяющего центры окружностей, описанных около оснований призмы.

5. Из указанных выше утверждений следует, что около любой правильной пирамиды и около любой правильной призмы можно описать шар.

6. Центр вписанного шара является точкой биссекторов (биссектор – плоскость, разбивающая двугранный угол на два равных угла) всех внутренних двугранных углов многогранников. Отсюда следует, что если вписанный шар существует, то только один.

7. Если цилиндр вписан в шар, то центр шара лежит на оси цилиндра.

8. Центр шара, вписанного в цилиндр, лежит на оси цилиндра.

9. Если шар описан около параллелепипеда, то все его грани должны быть прямоугольниками, то есть параллелепипед должен быть прямоугольным, а центр этого шара должен лежать в точке пересечения его диагоналей.

10. Если шар описан около призмы, то эта призма прямая, а ее основаниями служат такие многоугольники, около которых можно описать окружность.

11. Если шар описан около правильной пирамиды, то ее центр лежит на перпендикуляре к плоскости основании, проведенном через центр окружности, описанной около основания.

12. Если шар вписан в многогранник, то радиусы шара, проведенные в точке касания, перпендикулярны соответствующим граням многогранника.

13. Центр шара, вписанного в многогранник, равноудален от всех его граней.

14. Если шар вписан в правильную четырехугольную призму, то эта призма есть куб.

15. Центр шара, вписанного в правильную пирамиду, лежит в точке пересечения высоты с биссектрисой угла, образованного апофемой пирамиды и ее проекцией на плоскость основания.

Задачи

22.1В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

22.2Высота цилиндра 2. Радиус оснований 7. В этот цилиндр наклонно вписан квадрат так, что все его вершины лежат на окружностях оснований. Найти сторону квадрата.

22.3В конус радиуса и высотой 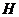вписан куб. Найти его ребро.

22.4В конус радиуса и высотой 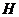вписана правильная треугольная призма, у которой все грани – квадраты. Найти ребро призмы.

22.5Полушар и вписанный в него конус имеют общее основание, и вершина конуса лежит на поверхности шара. Через середину высоты конуса проведена плоскость, параллельная основанию. Доказать, что площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, равна половине площади основания.

22.6Диагонали ромба 15 и 20. Шаровая поверхность касается всех его сторон. Радиус шара равен 10. Найти расстояние от центра шара до плоскости ромба.

22.7Тело ограничено двумя концентрическими сферами (полый шар). Доказать, что его сечение плоскостью, проходящей через центр, равновелико сечению, касательному к внутренней сфере.

22.8Найти радиус шара, описанного около правильной 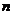-угольной пирамиды, если сторона основания равна 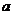, а боковое ребро наклонено к плоскости основания под углом .

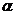22.9Правильная 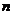-угольная призма вписана в шар радиуса . Ребро основания призмы равно 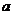. Найти высоту призмы при .

22.10 В шар радиуса вписана правильная треугольная пирамида с плоскими углами 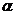при вершине. Найти высоту пирамиды.

Не нашли, что искали? Воспользуйтесь поиском: