Определения вписанных и описанных тел

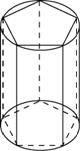
Призмой, вписанной в цилиндр, называется такая призма, у которой плоскостями оснований являются плоскости основания цилиндра, а боковыми ребрами – образующие цилиндра.

Призмой, описанной около цилиндра, называется призма, у которой плоскостями оснований являются плоскости основания цилиндра, а боковые грани касаются цилиндра.

Призма называется описанной около конуса, если одно основание конуса вписано в основания призмы, а вершина конуса лежат в плоскости верхнего основания призмы. Высоты призмы и конуса равны.

Призма называется вписанной в конус, если нижнее основание призмы лежит в основании конуса, а верхнее вписано в сечение конуса плоскостью, параллельной плоскости основания.

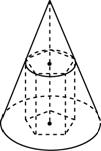
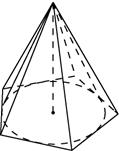
Пирамидой, вписанной в конус, называется пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды являются образующими конуса.

Пирамидой, описанной около конуса, называется пирамида, основание которой есть многоугольник, описанный около окружности основания конуса, а вершиной является вершина конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.

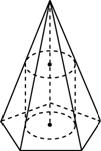
Пирамида называется описанной около цилиндра, если одно основание цилиндра лежит в плоскости основания пирамиды, а другое вписано в сечение пирамиды плоскостью, параллельной плоскости основания.

Пирамида называется вписанной в цилиндр, если основание пирамиды вписано в нижнее основание цилиндра и вершина пирамиды лежат в плоскости верхнего основания цилиндра. Высоты цилиндра и пирамиды равны.

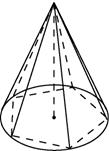
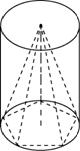
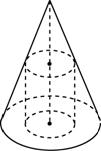
Конус называется описанным около цилиндра, если их оси совпадают, одно основание цилиндра лежит в плоскости основания конуса, а другое является сечением конуса плоскостью, параллельной плоскости основания.

Конус называется вписанным в цилиндр, если их основания совпадают, и вершина конуса лежат в плоскости верхнего основания цилиндра. Оси цилиндра и конуса совпадают, их высоты равны.

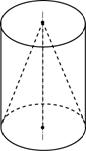
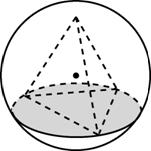
Многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара.

Многогранник называется описанным около шара, если все его грани касаются поверхности шара.

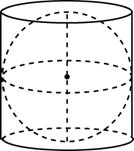
Цилиндр называют вписанным в шар, если окружности оснований лежат на поверхности шара.

Шар называют вписанным в цилиндр, если его поверхность касается боковой поверхности и оснований цилиндра. Диаметр шара является высотой цилиндра.

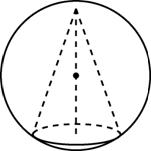
Конус называют вписанным в шар, если окружность основания и вершина конуса лежат на поверхности шара.

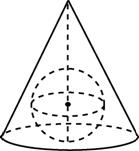
Шар называют вписанным в конус, если его поверхность касается боковой поверхности и основания конуса.

Не нашли, что искали? Воспользуйтесь поиском: