
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Объем усеченной пирамиды
Найдем объем усеченной пирамиды с площадями оснований  и
и  и высотой
и высотой  .
.

Пусть  – высота отсеченной пирамиды. Тогда
– высота отсеченной пирамиды. Тогда  – высота пирамиды, из которой получилась данная усеченная. Поскольку эта пирамида подобна отсеченной, то их основания относятся как квадрат коэффициента подобия, который равен
– высота пирамиды, из которой получилась данная усеченная. Поскольку эта пирамида подобна отсеченной, то их основания относятся как квадрат коэффициента подобия, который равен 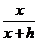 :
:
 .
.
Откуда

Объем усеченной пирамиды равен разности объемов полной и отсеченной пирамид:

Задачи
17.1Основание прямого параллелепипеда – ромб, площадь которого  кв. ед. Площади диагональных сечений
кв. ед. Площади диагональных сечений 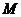 кв. ед. и
кв. ед. и  кв. ед. Найти объем параллелепипеда.
кв. ед. Найти объем параллелепипеда.
17.2В параллелепипеде длины трех ребер, исходящих из одной вершины, равны 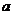 ,
,  ,
,  . Ребра
. Ребра 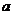 и
и  взаимно перпендикулярны, а ребро
взаимно перпендикулярны, а ребро  образует с каждым из них угол
образует с каждым из них угол 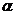 . Найти объем параллелепипеда.
. Найти объем параллелепипеда.
17.3Грани параллелепипеда – равные ромбы со стороной 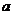 и острым углом 60о. Найти объем параллелепипеда.
и острым углом 60о. Найти объем параллелепипеда.
17.4Высота пирамиды  . На каком расстоянии от вершины находится сечение, параллельное основанию и делящее ее объем пополам.
. На каком расстоянии от вершины находится сечение, параллельное основанию и делящее ее объем пополам.
17.5По стороне основания 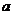 и боковому ребру
и боковому ребру  найдите объем правильной призмы: а) треугольной; б) четырехугольной; в) шестиугольной.
найдите объем правильной призмы: а) треугольной; б) четырехугольной; в) шестиугольной.
17.6В правильной шестиугольной призме площадь наибольшего диагонального сечения 4 кв. ед., а расстояние между двумя противоположными боковыми гранями 2. Найти объем призмы.
17.7Чему равен объем прямой четырехугольной призмы, если ее высота  , диагонали наклонены к плоскости основания под углами
, диагонали наклонены к плоскости основания под углами 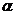 и
и  , а острый угол между диагоналями оснований равен
, а острый угол между диагоналями оснований равен  .
.
17.8По стороне основания 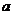 и боковому ребру
и боковому ребру  найдите объем правильной пирамиды: а) треугольной; б) четырехугольной; в) шестиугольной.
найдите объем правильной пирамиды: а) треугольной; б) четырехугольной; в) шестиугольной.
17.9Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое равно  . Найти объем пирамиды.
. Найти объем пирамиды.
17.10 Основание пирамиды – равнобедренный треугольник со сторонами 6, 6, 8. Все боковые ребра равны 9. Найти объем пирамиды.
17.11 В правильной усеченной четырехугольной пирамиде стороны нижнего и верхнего оснований равны 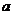 и
и  , а двугранный угол при ребре нижнего основания равен
, а двугранный угол при ребре нижнего основания равен 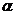 . Найти объем пирамиды.
. Найти объем пирамиды.
Тела вращения
Цилиндр
Не нашли, что искали? Воспользуйтесь поиском: