Построение сечения плоскостью, проходящей через заданные прямую и точку

Особое место занимают задачи построения сечения призмы и пирамиды плоскостями, проходящими через заданную точку на теле и заданную прямую в плоскости основания. Такая прямая называется следом секущей плоскости на плоскости основания. Для построения сечения достаточно построить отрезки пересечения секущей плоскости с гранями призмы или пирамиды.

Если известна какая-либо точка 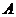на поверхности призмы или пирамиды, принадлежащая сечению, то сечение строиться по следующим правилам:

1. Если данная точка 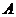принадлежит другому основанию призмы, то его пересечение с секущей плоскостью представляет собой отрезок, параллельный следу и содержащий данную точку;

2. Если данная точка 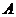принадлежит боковой грани призмы или пирамиды, то ее пересечение с секущей плоскостью строится так: сначала строиться точка пересечения следа и плоскости грани, затем строится отрезок на рассматриваемой грани, который является пересечением секущей плоскости и плоскости грани и содержит данную точку. Если грань, содержащая точку 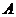, параллельна следу, то секущая плоскость пересекает эту грань по отрезку, параллельному следу и проходящему через точку .

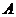Рассмотрим пример построения сечения призмы плоскостью со следом a, проходящей через точку .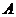

1. Проведем прямые через все ребра основания до пересечения с прямой 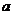. Обозначим точки пересечение , , , .

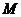2. Через точки и 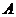проведем прямую. Точки ее пересечения с ребрами призмы обозначим за и .

3. Далее проведем прямую через точки и . Точку пересечения этой прямой с ребром обозначим .

4. Проведем прямую через точки и . Точку пересечения этой прямой с ребром обозначим .

5. Проведем прямую через точки и 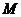. Точку пересечения этой прямой с ребром обозначим .

6. Получаем сечение призмы заданной плоскостью.

Задачи

16.1Построить сечения призмы плоскостью со следом a, проходящей через точку A.

16.2Построить сечение четырехугольной призмы плоскостью, проходящей через три точки на боковых ребрах призмы.

16.3Построить сечения пирамиды плоскостью со следом a, проходящей через точку A.

16.4В правильной четырехугольной призме площадь боковой грани равна . Найти площадь диагонального сечения.

16.5В правильной шестиугольной призме, у которой боковые грани – квадраты со стороной 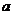, провести сечение через сторону нижнего основания и противолежащую ей сторону верхнего основания. Найти площадь полученного сечения.

16.6В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найти боковую поверхность призмы, если периметр сечения равен 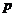, а боковые ребра равны .

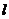16.7В правильной треугольной пирамиде с высотой через сторону основания 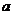проведена плоскость, пересекающая противолежащее ребро под прямым углом. Найти площадь сечения.

16.8По стороне основания 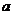найдите боковую поверхность правильной четырехугольной пирамиды, у которой диагональное сечение равновелико основанию.

16.9В правильной четырехугольной усеченной пирамиде сторона нижнего основания 8, верхнего – 5, высота равна 3. Провести сечение через сторону нижнего основания и противоположную вершину верхнего основания. Найти площадь этого сечения и двугранный угол между сечением и нижним основанием.

Не нашли, что искали? Воспользуйтесь поиском: