Определение и свойства пирамиды

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания.

Отрезки, соединяющие вершину пирамиды с вершинами оснований, называются ребрами пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Грани, не являющиеся основанием пирамиды, называются боковыми гранями. Все боковые грани пирамиды – треугольники. Пирамида называется n -угольной, если в ее основании лежит n -угольник. Треугольную пирамиду также называют тетраэдром.

Теорема 14.1. Если в пирамиде все высоты боковых граней, проведенные из вершины пирамиды равны, то

1. все боковые грани наклонены к плоскости основания под равными углами;

2. вершина пирамиды проектируется в центр окружности, вписанной в основание.

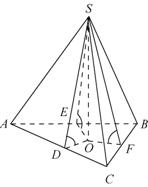
Доказательство. Рассмотрим пирамиду в которой высоты боковых граней равны 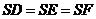. Проведем высоту пирамиды и рассмотрим треугольники 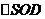, , . Это прямоугольные треугольники с общим катетом и равными гипотенузами 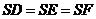, значит эти треугольники равны. Отсюда , т.е. равны углы наклона боковых граней к плоскости основания. Из равенства треугольников также следует равенство сторон , т.е. точка является центром вписанной в основание пирамиды окружности.

Теорема 14.2. Если в пирамиде все боковые ребра равны, то

1. все боковые ребра наклонены к плоскости основания под равными углами;

2. вершина пирамиды проектируется в центр окружности, описанной около основания.

Верны также обратные утверждения.

Усеченная пирамида

Проведем плоскость, параллельную основанию пирамиды и пересекающую эту пирамиды. Эта плоскость разделит пирамиду на два многогранника, один из которых представляет собой пирамиду меньшего размера и называется отсеченной пирамидой, второй – усеченной пирамидой.

Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями, остальные – боковыми гранями. Основания усеченной пирамиды являются подобными многоугольниками, а боковые грани представляют собой трапеции.

Теорема 14.3. Плоскость, параллельная основанию пирамиды, отсекает подобную пирамиду (без доказательства).

Не нашли, что искали? Воспользуйтесь поиском: