Правильная пирамида

Пирамида называется правильной, если ее основанием является правильной многоугольник и основание высоты совпадает с центром этого многоугольника. Очевидно, что у правильной пирамиды все боковые ребра равны, следовательно все ее боковые грани – равнобедренные треугольники.

Осью правильной пирамиды называется прямая, содержащая ее высоту. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой (). Все апофемы равны и являются биссектрисами и медианами боковых граней.

Теорема 14.4. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Доказательство. Боковые грани правильной пирамиды есть равные треугольники, основания которых 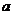являются сторонами многоугольников в основаниях пирамиды, а апофемы 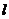являются высотами боковых граней пирамиды. Тогда по определению площадь боковой поверхности:

,

где – периметр основания правильной n -угольной пирамиды.

Усеченная пирамида, которая получается из правильной, также называется правильной. Боковыми гранями правильной усеченной пирамиды являются равнобокие трапеции, их высоты называются апофемами.

Задачи

14.1Доказать, что боковые ребра правильной треугольной пирамиды перпендикулярны противоположным ребрам основания.

14.2Доказать, что основание перпендикуляра, опущенного из вершины 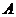основания правильной треугольной пирамиды на боковую грань , лежит на высоте этой боковой грани.

14.3Основание пирамиды – равнобедренный треугольник с основанием 12 и боковой стороной 10. Боковые грани образуют с основанием двугранные углы 45^о. Найти высоту пирамиды (ответ: 3).

14.4Основание пирамиды – ромб с диагоналями 6 и 8, высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1. Найти боковую поверхность пирамиды (ответ: 26).

14.5Основание пирамиды – квадрат, ее высота проходит через одну из вершин основания. Найти боковую поверхность пирамиды, если сторона основания равна 20, а высота 21 (ответ: 10).

14.6В треугольной пирамиде все ребра равны. Найти угол между скрещивающимися медианами двух соседних граней.

14.7Найти боковую поверхность усеченной правильной пирамиды.

14.8Высота пирамиды равна 16. Площадь основания равна 512. Найти высоту усеченной пирамиды, меньшее основание которой равно 50.

14.9По стороне основания 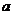и высоте найти полную поверхность правильно пирамиды а) треугольной, б) четырехугольной, в) шестиугольной.

14.10 В правильной четырехугольной пирамиде плоский угол при вершине равен 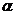. Найти двугранный угол при основании пирамиды

14.11 В правильной усеченной четырехугольной пирамиде стороны оснований равны 8 и 2, высота равна 4. Найти полную поверхность пирамиды.

14.12 Доказать, что боковая поверхность правильной усеченной пирамиды равна произведению полсуммы периметров оснований на апофему.

Не нашли, что искали? Воспользуйтесь поиском: