Объем шарового сектора и шарового сегмента

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

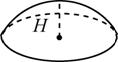
Формула для объема шарового сегмента высотой 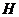получается аналогично формуле для объема шара:

Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, вершиной которого является центр шара, а основание совпадает с основанием сегмента.

Объем шарового сектора получается как сумма объемов сегмента высотой 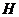и конуса с радиусом основания 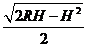и высотой :

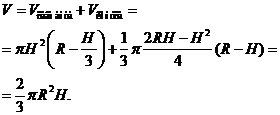
Задачи

23.1В цилиндр вписана правильная треугольная призма, а в призму вписан цилиндр. Найти отношение объемов цилиндров.

23.2Осевым сечение конуса является равнобедренный прямоугольный треугольник с площадью 9. Найти объем конуса.

23.3Равносторонний треугольник вращается вокруг своей стороны 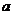. Найти объем полученного тела вращения.

23.4Найти объем усеченного конуса с радиусами оснований и и высотой .

23.5Усеченный конус, у которого радиусы оснований 4 и 22, и равновеликий цилиндр имеют одинаковую высоту. Чему равен радиус основания цилиндра?

23.6Из деревянного цилиндра, высота которого равна диаметру основания, выточен наибольший шар. Сколько процентов материала сточено?

23.7Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

23.8Диаметр шара, равный 30, является осью цилиндра, у которого радиус основания равен 12. Найти объем части шара, заключенной внутри цилиндра.

23.9Шар радиуса 10 цилиндрически просверлен по оси. Диаметр отверстия равен 12. Найти объем тела.

23.10 Полукруг свернут в коническую поверхность. Найти угол между образующей и осью конуса.

23.11 Доказать, что полная поверхность равностороннего конуса равновелика поверхности шара, построенного на его высоте как на диаметре.

Не нашли, что искали? Воспользуйтесь поиском: