Оценка погрешности приближения

Оценим точность приближения x_{n .} Получим сначала общую формулу.

Теорема 3. Пусть ξ – точный, а - приближенный корни уравнения (1), , причем при . Тогда справедлива оценка

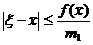. (6)

Доказательство. Применяя теорему Лагранжа, будем иметь:

, где . Переходя к модулям, получим:

. Отсюда следует оценка (6).

Выведем еще одну формулу для оценки точности приближения x_n. Применяя формулу Тейлора, имеем

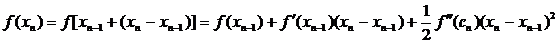, (7)

где .

Из равенства (7) следует, что 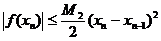, где . Следовательно, на основании формулы (6) окончательно получаем оценку

, (8)

где , .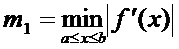

Установим также формулу, связывающую абсолютные погрешности двух последовательных приближений x_n и x_n+1. Из формулы (5) получаем

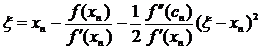или . Отсюда

. (9)

Это означает, что если, например, и , то из оценки (9) следует, что , т.е. в этом случае если приближение x_n имело m верных знаков после запятой, то следующее приближение x_{n +1} будет иметь по меньшей мере 2 m верных знаков после запятой. Иными словами, если μ≤1, то при вычислениях с помощью метода Ньютона число верных знаком после запятой удваивается на каждом шаге.

Не нашли, что искали? Воспользуйтесь поиском: