Л5 Решение систем линейных алгебраических уравнений.

Классификация численных методов решения систем линейных алгебраических уравнений.

К решению систем линейных алгебраических уравнений с большим числом неизвестных приводят многие практически важные задачи. Достаточно сказать, что решение краевых задач для уравнений в частных производных сводится к решению систем линейных алгебраических уравнений с большим числом неизвестных. Однако способов, одинаково эффективных и пригодных для решения всех систем, не существует. Поэтому разработано множество методов, предназначенных для решения систем с матрицей того или иного специального вида. Все эти методы можно разделить на два больших класса: прямые (или точные) и итерационные.

Прямые методы характеризуются тем, что дают решение системы за конечное (иногда неприемлемо большое) число арифметических операций. Если коэффициенты системы не содержат погрешностей, а арифметические операции выполняются точно (без округления), то решение получается точным. К прямым методам относятся: метод Гаусса и его многочисленные модификации (например, метод главного элемента, метод квадратного корня, метод отражений и т.д.), метод Крамера, имеющий больше теоретическое значение; методы ортогонализации. Недостатки прямых методов: они могут потребовать выполнения неприемлемо большого числа арифметических и логических операций; погрешности округления могут очень сильно исказить результат.

Итерационные методы позволяют получить приближенное решение с любой заданной точностью ε. Они дают искомое решение как предел последовательности приближений и различаются способами построения таких последовательностей. К итерационным методам относятся метод простой итерации, метод Зейделя, релаксационные методы, методы подпространств Крылова и многие другие.

Метод Гаусса решения систем линейных алгебраических уравнений

Дана система линейных алгебраических уравнений

с квадратной неособенной матрицей, - неизвестные. Метод Гаусса (метод последовательного исключения неизвестных) состоит из прямого и обратного хода. В результате прямого хода матрица системы за n шагов приводится к верхнему треугольному виду, а обратного - вычисляются значения неизвестных.

Формулы прямого хода метода Гаусса имеют вид

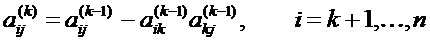
Формулы обратного хода метода Гаусса имеют вид

,

где верхний индекс обозначает номер шага.

Метод Гаусса имеет множество модификаций, обусловленных, главным образом, свойствами матрицы системы: метод Гаусса с выбором главного элемента, метод квадратного корня, метод отражений и т.д. Очень часто используется метод прогонки, который применяется для решения систем с трех- или пятидиагональной матрицей.

Не нашли, что искали? Воспользуйтесь поиском: