Л4….РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

МЕТОД НЬЮТОНА

I. Рассмотрим сначала систему двух уравнений

f ₁(x, y)=0

(1)

f ₂(x, y)=0

Обозначим через ξ и η компоненты точного решения этой системы, а через x_n, y_n - компоненты приближенного решения. Положим ξ= x_n +Δ x_n, η= y_n +Δ y_n. Тогда

f ₁(x_n +Δ x_n, y_n +Δ y_n)=0

(2)

f ₂(x_n +Δ x_n, y_n +Δ y_n)=0

Отсюда, применяя формулу Тейлора и ограничиваясь линейными членами относительно Δ x_n, Δ y_n, получим

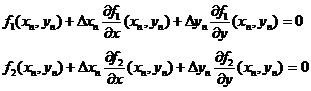(3)

Система (3) представляет собой систему линейных алгебраических уравнений относительно неизвестных Δ x_n, Δ y_n с матрицей

Такая матрица называется матрицей Якоби, а ее определитель – якобианом. Если якобиан отличен от нуля, то систему (3) можно решить и положить

x_{n+ 1} = x_n +Δ x_n

y_{n+ 1} = y_n +Δ y_n

Вычисления прекращаются по условию .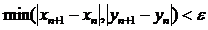

II. В общем случае систему нелинейных уравнений можно записать в векторной форме

f (x)=0 (1)

или более подробно в координатном виде

f_k (x ₁, x ₂,…, x_n)=0, k =1, 2, …, n

Пусть известно некоторое приближение x ^s к решению x и x = x ^s +Δ x. Разлагая функции в левых частях уравнений (1) и ограничиваясь первыми производными, т.е. линеаризуя уравнения, получаем

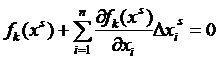, k =1, 2, …, n или 2)

Таким образом, решение системы нелинейных уравнений сводится к решению системы линейных алгебраических уравнений. Далее полагаем x ^{s+ 1} = x ^s +Δ x ^s (3)

и продолжаем процесс вычислений, пока не выполнится условие || x ^s+1- x ^s||<ε.

Так же, как в случае одного уравнения, проводится теоретический анализ условий сходимости. Однако достаточное условие сходимости имеет настолько сложный вид, что проверить его выполнение практически никогда не удается. Поэтому на практике используют следующий результат: в достаточно малой окрестности решения итерации сходятся, если якобиан отличен от нуля, причем сходимость квадратичная.

Следовательно, если нулевое приближение выбрано удачно, то метод Ньютона сходится, причем очень быстро. Нулевое приближение в случае двух переменных можно найти графически. Для трех и более переменных (а также комплексных корней) удовлетворительных способов подбора нулевых приближений нет.

Не нашли, что искали? Воспользуйтесь поиском: