Метод простой итерации решения систем линейных алгебраических уравнений

Дана система линейных алгебраических уравнений, которую в векторно-матричном виде можно записать

Ax=b. (1)

Здесь матрица A – заданная квадратная неособенная матрица, так что система (1) имеет единственное решение, b – заданный вектор (правая часть), x – искомый вектор.

Эквивалентными преобразованиями приведем систему (1) к виду

x = αx + β (2)

где α – матрица той же размерности, что и А, а β – вектор, так что решение системы (1) является решением системы (2) и, наоборот, решение системы (2) является решением системы (1).

Выберем некоторый начальный вектор x^{( 0)} и построим итерационный процесс, который называется методом простой итерации

x^{( k+1)}= αx^{( k)}+ β, k =0, 1, … (3)

Достаточное условие сходимости метода простой итерации дает следующая теорема: Процесс итерации (3) для приведенной системы (2) сходится к ее единственному решению, если какая-нибудь норма матрицы α меньше 1.

Таким образом, для итерационного процесса (3) при произвольном x^{( 0)} достаточное условие сходимости есть .

Доказательство. Пусть 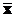- точное решение системы (2), т.е.

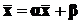(4)

Вычитая из равенства (4) равенство (3), получаем

. (5)

Применяя формулу (5) при k =0, 1, … получаем

,

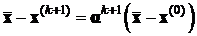следовательно, .

Если стремится к нулю при 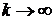, то 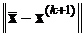стремится к нулю при любом начальном векторе . А так как , при 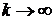(это следует из свойств нормы матрицы).

Этим доказана сходимость итерационного процесса. Кроме того, используя (5), можно записать (E - α) x = β, следовательно, x = αx + β, т.е. предельный вектор x является решением системы (2). Так как матрица E - α неособенная, то решение x единственно.

Следствие 1. Процесс итерации для системы (2) сходится, если

a) ; b) или c)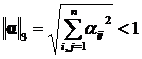

Следствие 2. Для системы 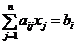, i =1, 2, …, n (6)

процесс итерации сходится, если выполнены неравенства 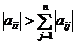при j ≠ i, i= 1, 2, …, n.

Не нашли, что искали? Воспользуйтесь поиском: