Л6 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

1. Вводные замечания. В вычислительной практике часто приходится иметь дело с функциями f (x), заданными таблицами их значений для некоторого конечного множества значений аргумента x на отрезке [ a, b ], x ₀= a, x_m = b.

Таб.1

Здесь использованы обозначения y ₀= f (x ₀), y ₁= f (x ₁), …, y_m = f (x_m).

Эта таблица может быть получена, например, в результате измерения некоторой величины в определенные моменты времени и т.д.

В процессе решения задачи оказывается необходимым использовать значения f (x) для промежуточных значений аргумента, которых нет в таблице. В этом случае заданную функцию заменяют некоторой приближенной функцией. Такую функцию можно искать из различных соображений. Одним из подходов является следующий. Строят функцию φ (x), достаточно простую для вычислений, которая в заданных точках x ₀, x ₁, …, x_m принимает значения y ₀, y ₁, …, y_m, а в остальных точках отрезка [ a, b ] приближенно представляет функцию f (x) с той или иной степенью точности и при решении задачи заменяет функцию f (x). Задача построения такой функции φ (x) называется задачей интерполирования. Чаще всего интерполирующую функцию φ (x) отыскивают в виде алгебраического полинома.

Интерполирование применяется и в том случае, когда для функции f (x) известно ее аналитическое представление, но вычисление каждого значения требует большого числа операций. Если в процессе решения задачи необходимо находить значения f (x) для очень большого числа значений аргументов, то для сокращения объема вычислений прибегают к интерполированию. Для этого вычисляют несколько значений f (x_i), i =0, 1, …, m и по ним строят интерполяционную функцию φ (x), с помощью которой и вычисляют приближенные значения f (x) в остальных точках.

2. Математическая постановка задачи интерполирования заключается в следующем. Пусть R - пространство действительных функций, определенных на отрезке [ a, b ], и { φ_i } - заданная конечная или счетная система функций из R, такая, что их любая конечная подсистема является линейно-независимой. Примерами таких систем являются 1) последовательность степеней x 1, x, x ², x ³, …; 2) последовательность тригонометрических функций 1, sin x, cos x, sin 2 x, cos 2 x, …; 3) последовательность показательных функций 1, 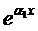, , …, где { α_i } – некоторая числовая последовательность, и т.д. Возьмем первые n +1 элементов { φ_i } и образуем всевозможные линейные комбинации с действительными коэффициентами a_i. Каждая такая комбинация принадлежит пространству R. Множество всех линейных комбинаций само является линейным пространством, обозначим его .

Произвольной функции из R надо поставить в соответствие функцию из . Задача интерполирования формулируется так: для данной конечной совокупности точек 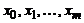(x_i ≠ x_j при i≠j), принадлежащих отрезку [ a,b ], и данной функции f (x) из R найти функцию φ из так, чтобы в заданных точках значения f и φ совпадали. Другими словами, определить константы 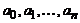так, чтобы имели место равенства

. (1)

Тогда функция называется интерполирующей функцией, а точки 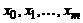- узлами интерполяции.

3. Построение интерполирующей функции. Для построения интерполирующей функции следует выбрать систему функций { φ_i (x)}, зафиксировать число n и определить коэффициенты a_i. Для определения коэффициентов a_i имеем систему (1) m +1 уравнения с n +1 неизвестными. Матрица этой системы имеет вид:

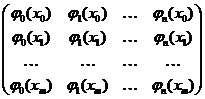
Для того, чтобы коэффициенты a_i можно было подобрать для любой функции f, нужно потребовать, чтобы ранг матрицы этой системы был равен m +1. При этом n ≥ m. Далее, чтобы решение задачи было однозначным, надо потребовать, чтобы n = m. Итак, в дальнейшем будем предполагать, что n = m и определитель системы (1) отличен от нуля. Тогда при любых f (x_j) система (1) будет иметь решение и притом единственное.

4. Интерполирование при помощи алгебраических полиномов. Если {φ_i} – степени , то говорят об алгебраической интерполяции, а функцию φ(x) называют интерполяционным полиномом. Функции , составляющие последовательность { φ_i } в этом случае, линейно независимы на любом отрезке. Действительно, если бы на каком-то отрезке имело место тождественное равенство , то все c_i =0, так как алгебраический многочлен степени n с ненулевыми коэффициентами не может иметь больше n корней. При n=m для любого набора значений f (x_j)можно построить интерполяционный полином степени n и притом только один. Действительно, в этом случае определитель системы линейных алгебраических уравнений (1) является определителем Вандермонда и отличен от нуля.

,

так как среди узлов интерполяции нет двух совпадающих точек. Следовательно, решение системы (1) существует, оно единственно и коэффициенты интерполяционного полинома определяются однозначно.

5. Интерполяционный полином Лагранжа. Построение интерполяционного полинома путем решения системы (1) не всегда удобно на практике, поэтому стремятся получить явные выражения для коэффициентов интерполяционного полинома.

Пусть - узлы интерполяции, - заданные значения функции в этих узлах. Обозначим искомый полином через и будем искать его в виде

,

где является полиномом n -й степени, удовлетворяющим следующему условию:

(2)

Положим , при этом удовлетворяет второму из условий (2). Коэффициент c_i подберем так, чтобы полином удовлетворял первому из условий (2):

.

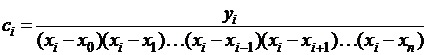Тогда интерполяционный полином Лагранжа принимает вид:

. (3)

Введем обозначение: . Тогда полином Лагранжа можно записать в виде

. (4)

6. Численное интерполирование. Полином Ньютона. Интерполяционный полином Ньютона применяется в том случае, когда таблица функции задается с постоянным шагом. Пусть - заданные точки, - шаг таблицы, - заданные значения (). При построении интерполяционного полинома Ньютона используются конечные разности. Конечной разностью первого порядка называется величина , конечной разностью k-го порядка называется величина .

Интерполяционный полином Ньютона будем искать в виде где - коэффициенты, которые требуется определить. Используем для этого определение интерполяционного полинома. Так как , то . Далее . Следовательно, . Продолжая таким образом, получаем , и полином Ньютона имеет вид

(8)

Для некоторых функций f(x) конечные разности с ростом их порядка уменьшаются по абсолютной величине, так что начиная с некоторого номера k, слагаемые в формуле (13) можно не учитывать. В результате уменьшается степень полинома и сокращается объем необходимых вычислений, однако при этом используется не вся заданная таблица. Поэтому в этом случае применять формулу (13) можно лишь для вычисления значений функции ближе к началу заданной таблицы, т.е. для вычисления искомого значения в точке, принадлежащей отрезку из используемой части таблицы. Для интерполирования вблизи конца таблицы применяется вторая форма полинома Ньютона:

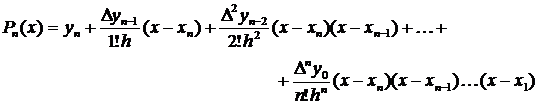
7. Оценка остаточного члена интерполяционного полинома. Погрешность интерполяционного полинома . В узлах интерполяции , в остальных точках эта функция отлична от нуля. Для получения формулы оценки погрешности предположим, что функция n +1 раз непрерывно дифференцируема, и рассмотрим функцию

(5)

Эта функция имеет n +1 корень в узлах интерполяции, подберем коэффициент k так, чтобы в некоторой точке 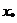функция u (x) имела n +2 корень:

. (6)

Предположим, что . Тогда функция принимает нулевые значения на концах каждого из (n +1) интервала [ ], [ ],…,[ ],[ ],…,[ ]. Тогда согласно теореме Ролля первая производная имеет по крайней мере n +1 корень, вторая производная 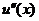имеет по крайней мере n корней и, наконец, (n +1)-я производная имеет по крайней мере один корень. Обозначим этот корень через ξ: . Продифференцируем выражение (5) (n +1) раз:

Подставив , получим

Отсюда

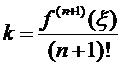(7)

Приравнивая правые части равенств (6) и (7), получим

.

Учитывая, что - произвольная точка и введя обозначение 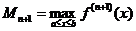, получим окончательно

.

8. Выбор узлов интерполирования. Отклонение интерполяционного полинома 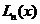от заданной функции f (x) определяется величиной и . Величину в некоторых случаях мы можем менять по нашему желанию, изменяя точки x_i. Поставим следующую задачу: выбрать узлы x_i так, чтобы был наименьшим. Для решения этой задачи используются полиномы Чебышева.

Полином Чебышева определяется следующим образом: . При n = 0 T ₀(x)=1, n =1 – T ₁(x) = cos(arccos x) = x. Далее из тождества

,

полагая θ = arccos x,получим T_{n +1}(x) = 2 xT_n (x)– T_{n -1}(x). Таким образом, T_n (x) действительно являются многочленами n -й степени, причем коэффициент при xⁿ равен 2 ^{n -1}.

Примеры многочленов Чебышева: T ₂(x)=cos(2arccos x)=2cos²(arccos x)–1=2 x ²–1,

T ₃(x)=4 x ³–3 x, T ₄(x)=8 x ⁴–8 x ²+1, T ₅(x)=16 x ⁵–20 x ³+5 x и т.д.

Многочлен n -й степени T_n (x) имеет ровно n корней. Из cos(n arccos x)=0 следует или 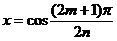. При m =0, 1, …, n –1 получим n различных корней, причем все они принадлежат отрезку [-1,1]. Заметим также, что и достигается n +1 раз в точках

(*)

Если в качестве отрезка интерполирования взять [–1,1], а узлов интерполирования – корни многочлена Чебышева T_n (x), то 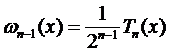и .

Покажем, что какой бы многочлен P_n (x) со старшим коэффициентом 1 мы ни взяли, . Действительно, если бы это было не так, разность представляла бы собой многочлен степени n -1, принимающий в n +1 точках (*) попеременно то положительные, то отрицательные значения. Следовательно, он должен иметь по крайней мере n корней, что невозможно.

Таким образом, если ограничиться рассмотрением отрезка [–1,1] и в качестве узлов интерполирования взять нули многочлена Чебышева, то оценка погрешности интерполяционного полинома примет вид: , так как .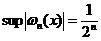

Если интерполирование производится на произвольном отрезке [a,b], то линейной заменой переменной , его можно перевести в [–1,1]. При этом корни многочлена T_n (x) перейдут в точки

Оценка для этого случая будет такой: .

Многочлены называются многочленами, наименее отклоняющимися от нуля.

9. Обратное интерполирование. Часто на практике возникает задача об отыскании по заданному значению функции значения аргумента. Эта задача решается методами обратного интерполирования. Здесь возможны два случая.

1. Заданная функция является монотонной. Обратное интерполирование в этом случае легче всего осуществить путем замены функции аргументом и обратно и последующего интерполирования.

2. Заданная функция не является монотонной. В этом случае, не меняя местами аргументы и функцию, записываем ту или иную интерполяционную формулу; затем, используя известные значения аргумента и считая функцию известной, решаем полученное уравнение относительно неизвестной.

Оценка остаточного члена при использовании первого приема будет такой же, как при прямом интерполировании, только производные от прямой функции заменятся на производные от обратной функции.

Оценим погрешность второго метода. Если f (x) – заданная функция и L_n (x) – полином Лагранжа, построенный для этой функции по узлам , то

(*)

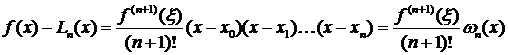Предположим, что надо найти , такое что задано). Решая уравнение 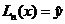, найдем некоторое значение . Подставляя его в равенство (*), получаем

.

Применяя формулу Лагранжа (конечных приращений), будем иметь

, где . Если [ a, b ] – интервал, содержащий , и , то из последнего выражения следует 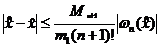. При этом предполагается, что уравнение 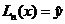мы решили точно.

Отметим в заключение, что решение уравнения f (x)=0 можно свести к задаче обратного интерполирования. Для этого нужно составить таблицу значений y = f (x), а затем применить обратное интерполирование, отыскивая значение x, соответствующее y =0.

Не нашли, что искали? Воспользуйтесь поиском: