Оценка погрешности приближений процесса Зейделя по первой норме

Пусть x^{( k )} и x^{( k+1 )} (k ≥0) – два последовательных приближения решения системы (2), полученные по методу Зейделя. Применяя к ним преобразования, использованные при доказательстве теоремы о первом достаточном условии сходимости метода Зейделя, получим неравенство, аналогичное (14): 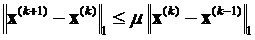. Отсюда, используя свойства нормы, получаем

.

(Здесь использована формула суммы p членов геометрической прогрессии

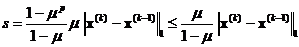, так как μ <1).

при p →∞, 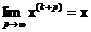, следовательно,

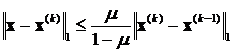, (16)

где μ вычисляется по формуле (15). Таким образом, условие прекращения вычислений для получения решения с точностью ε в процессе Зейделя имеет вид:

.

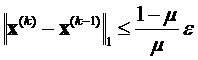В частности, из неравенства (16) можно получить оценку , которая позволяет оценить число итерационных шагов, необходимых для достижения требуемой точности.

Не нашли, что искали? Воспользуйтесь поиском: