Оценка погрешности приближений процесса итерации

Пусть x^{( k -1)} и x^{( k )} (k ≥1) – два последовательных приближения решения системы (2). При p ≥1 можно записать

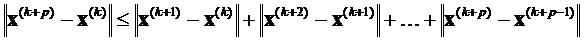(7)

Так как x^{( m+1)}= αx^{( m )}+ β и x^{( m )}= αx^{( m -1)}+ β, то x^{( m +1)}- x^{( m )}= α (x^{( m )}- x^{( m -1)}) и, следовательно, 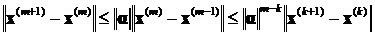при m > k ≥1. Поэтому из формулы (7) получаем

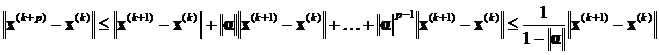. Переходя к пределу при p →∞, получим окончательно

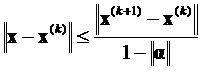при k ≥1 (8)

или

Отсюда получается условие завершения вычислений. Введем обозначение 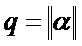. Для получения приближенного решения x ^k системы (2) с заранее заданной точностью ε вычисления следует продолжать до выполнения условия

.

И только в частном случае q <0.5 вычисления прекращаются при выполнении условия .

Метод Зейделя

Метод Зейделя является модификацией метода простой итерации, он основан на идее использовать уже вычисленные компоненты нового приближения при вычислении очередной его компоненты. Вычислительная схема метода Зейделя записывается в виде:

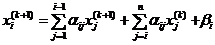, i =1, 2, …, n; k =0, 1, …

Доказательство достаточного условия сходимости этого метода использует конкретный вид нормы, поэтому соответствующие теоремы формулируются отдельно для каждой нормы. Рассмотрим первое достаточное условие сходимости метода Зейделя.

Теорема. Если для системы (2) выполнено условие

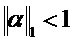(9)

то процесс Зейделя для системы (2) сходится к ее единственному решению при любом выборе начального вектора x^{( 0)}.

Доказательство. Пусть x^{( k)} – k -е приближение процесса Зейделя. Тогда можно записать:

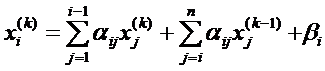, i =1, 2, …, n; k =1, 2, … (10)

При выполнении условия (9) система (2) допускает единственное решение x, которое может быть найдено, например, методом простой итерации, т.е.

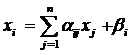, i =1, 2, …, n (11)

Вычитая равенство (10) из равенства (11), получим

.

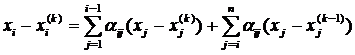Отсюда

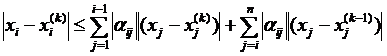(12)

Согласно смыслу принятой нормы 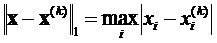. Поэтому для j =1, 2, …, n. Следовательно, из неравенства (12) выводим:

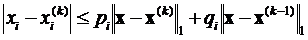(13)

где , .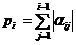

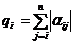Пусть s = s (k) есть то значение индекса i, при котором достигается максимум . Полагая i = s в неравенстве (13), получим

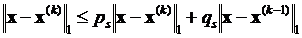или .

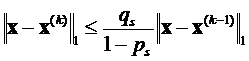Отсюда

(14)

где . (15)

Покажем, что μ ≤║ α ║₁<1. Действительно, так как , то 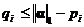и следовательно, 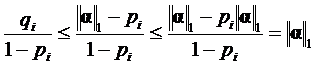. Поэтому μ ≤║ α ║₁<1.

Из неравенства (14) вытекает, что и, значит, , тем самым сходимость процесса Зейделя к искомому решению доказана.

Замечание. Так как для метода простой итерации , а для метода Зейделя , где μ ≤║ α ║₁, то в условиях теоремы 1 сходимость процесса Зейделя в общем несколько лучше, чем сходимость метода простой итерации. Из формулы (15) следует, что при применении метода Зейделя систему (2) выгодно располагать таким образом, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов .

Не нашли, что искали? Воспользуйтесь поиском: