Л7 Численное интегрирование.

Если функция f (x) непрерывна на отрезке [ a,b ] и известна ее первообразная f (x), то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница

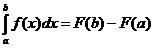(1)

Однако во многих задачах первообразная f (x) не может быть найдена с помощью элементарных функций или является слишком сложной. В таких случаях применение формулы (1) становится затруднительным или невозможным. Кроме того, на практике подынтегральная функция f (x) часто задается таблично, и тогда само понятие первообразной теряет смысл. Поэтому большое значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.

Задача численного интегрирования функции заключается в необходимости вычисления значений определенного интеграла, когда известен ряд значений подынтегральной функции.

Численное вычисление однократного интеграла называется механической квадратурой, а двойного – механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными.

Обычный прием механической квадратуры заключается в том, что данную функцию f (x)на рассматриваемом отрезке [ a,b ] заменяют интерполирующей или другой аппроксимирующей функцией φ(x) простого вида (например, полиномом), а затем приближенно полагают

. (2)

φ(x)такова, что интеграл в правой части (2) вычисляется непосредственно (по формуле (1)).

Не нашли, что искали? Воспользуйтесь поиском: