Квадратурная формула Гаусса

Формулы Ньютона-Котеса получены в предположении, что узлы интерполяции располагаются на отрезке интегрирования равномерно, с постоянным шагом. Но в том случае, когда подынтегральная функция f (x) задается в аналитическом виде, можно выбрать количество узлов n и расположить эти узлы произвольным образом. Очевидно, что чем меньше число n, тем меньше объем вычислений. Так как погрешность интерполяционного полинома зависит от расположения узлов интерполяции, можно предположить, что для вычисления значения интеграла тоже существует некоторое оптимальное расположение узлов, при котором погрешность результата является минимальной. Найдем такое оптимальное расположение.

Рассмотрим функцию f (x), заданную на стандартном отрезке [–1,1]. Общий случай легко получить путем линейной замены независимой переменной.

Поставим задачу: подобрать точки x ₁, x ₂, …, x_n и коэффициенты A ₁, A ₂, …, A_n так, чтобы квадратурная формула

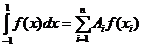(1)

была точной для всех полиномов f (x) наивысшей возможной степени N.

Так как мы имеем 2 n постоянных x ₁, x ₂, …, x_n и A ₁, A ₂, …, A_n, а полином степени 2 n –1 определяется 2 n коэффициентами, то в общем случае наивысшая степень N = 2 n –1. Для обеспечения выполнения равенства (1) для любого полинома необходимо и достаточно, чтобы оно было верным при f (x)=1, x, x ², …, x ^{2 n -1}. Действительно, полагая

(k =0, 1, …, 2 n -1) (2)

и будем иметь .

Таким образом, учитывая соотношения

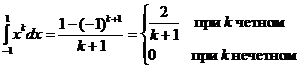
заключаем, что для решения поставленной задачи достаточно определить x_i и A_i из системы 2 n уравнений

(3)

Система (3) является нелинейной, и ее решение обычным путем представляет большие математические трудности. Использование полиномов Лежандра позволяет свести решение системы (3) к решению системы линейных алгебраических уравнений.

Некоторые сведения о полиномах Лежандра. Полиномами Лежандра называются полиномы вида , n =0, 1, ….Например, пять первых полиномов Лежандра имеют вид: P ₀(x)=1; P ₁(x)= x; P ₂(x)= , P ₃(x)= P ₄(x)=

Важнейшие свойства полиномов Лежандра

1) P_n (1)=1; P_n (–1)=(–1) ⁿ; n =0, 1, …

2) при k < n, где Q_k (x) – любой полином степени k < n

3) полином Лежандра P_n (x) имеет n различных и действительных корней, которые расположены на отрезке [ – 1,1].

Вернемся к решению системы (3). Рассмотрим полиномы f (x)= x^k P_n (x), k =0, 1, …, n –1, где P_n (x) – полином Лежандра.

Так как степени этих полиномов не превышают 2 n –1, для них справедлива формула (1) и

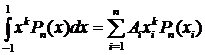(k =0, 1, …, 2 n –1) (4)

С другой стороны, в силу ортогональности полиномов Лежандра (свойство 2) выполнены равенства при k < n, поэтому

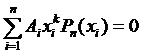, k =0, 1, …, n –1 (5)

Равенства (5) заведомо будут обеспечены при любых значениях A_i, если положить P_n (x_i)=0, i =0, 1, …, n. Это означает, что для достижения наивысшей точности квадратурной формулы (1) в качестве точек x_i достаточно взять нули соответствующего полинома Лежандра. Согласно свойству 3, эти нули действительны, расположены на интервале (– 1,1) и различны. Зная x_i, из линейной системы первых n уравнений системы (3) можно найти коэффициенты A_i, i =0, 1, …, n. Определитель этой системы является определителем Вандермонда

и, следовательно, A_i определяются однозначно.

Формула (1), где x_i – нули полинома Лежандра P_n (x) и A_i определяются из системы (3), называется квадратурной формулой Гаусса.

Неудобство применения квадратурных формул Гаусса состоит в том, что точки x_i и коэффициенты A_i – вообще говоря, иррациональные числа. Этот недостаток отчасти искупается ее высокой точностью при сравнительно малом числе точек.

Остаточный член формулы Гаусса с n узлами выражается следующим образом:

Отсюда и т.д.

Не нашли, что искали? Воспользуйтесь поиском: