Л8 Численное дифференцирование

Численное дифференцирование применяется, если функцию y = f (x) трудно или невозможно продифференцировать аналитически – например, если она задана таблично. Оно используется также при решении дифференциальных уравнений разностными методами.

При численном дифференцировании функцию f (x) аппроксимируют легко вычисляемой функцией φ(x) и полагают, что 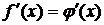. При этом можно использовать различные способы аппроксимации. Мы рассмотрим простейший случай – аппроксимацию интерполяционным полиномом Ньютона. Введя обозначение t_i = x–x_i, запишем полином Ньютона и продифференцируем его:

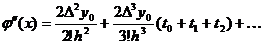
Общая формула имеет вид: 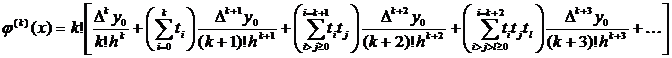(1)

Обрывая ряд на некотором числе членов, получим приближенное выражение для соответствующей производной. Наиболее простые выражения получим, оставляя в формуле (1) только первый член:

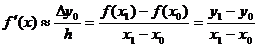
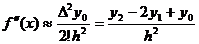(2)

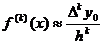
Исследуем точность полученных выражений. Если шаг таблицы достаточно мал, то погрешность будет близка к первому отброшенному члену. Пусть мы используем узлы x_i, i =0,1,…, n. Тогда первый отброшенный член содержит конечную разность 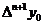и – погрешность в узле с номером k.

Таким образом, порядок точности формулы (1) по отношению к шагу таблицы равен числу оставленных в ней членов, или, что то же самое, он равен числу узлов интерполяции минус порядок производной. Поэтому минимальное число узлов, необходимое для вычисления k -й производной, равно k +1; оно приводит к формулам (2) и обеспечивает первый порядок точности. Эти выводы соответствуют общему принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.

Не нашли, что искали? Воспользуйтесь поиском: