Лекция№10 Метод Рунге-Кутта. Алгоритм и оценка погрешности

Метод Рунге-Кутта позволяет строить схемы различного порядка точности. Эти схемы очень удобны для программирования. В настоящее время они являются наиболее употребительными в практических вычислениях. Рассмотрим метод Рунге-Кутта на примере задачи Коши для обыкновенного дифференциального уравнения первого порядка.

Пусть дана задача (1)-(2). Требуется определить приближенные значения y в точке 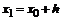, где h –шаг сетки.

Определение 1. Пусть s – положительное целое число (число стадий или этапов) и 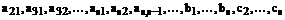- вещественные коэффициенты. Тогда метод

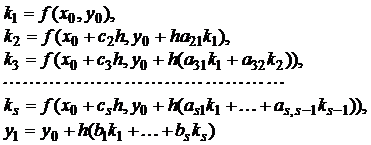(3)

называется s-стадийным (s-этапным) явным методом Рунге-Кутта для задачи (19)-(20).

Обычно коэффициенты c_i удовлетворяют условиям

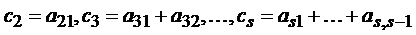
Определение 2. Метод Рунге-Кутта (3) имеет порядок p, если для достаточно гладких задач (1)-(2)

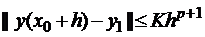
Вывод общих формул Рунге-Кутта требует довольно громоздких выкладок. Поэтому рассмотрим в качестве примера без вывода 4-стадийный метод, имеющий порядок p =4, называемый классическим методом Рунге-Кутта. Выберем шаг h и введем обозначения: 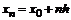и 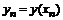. Тогда классический метод Рунге-Кутта имеет вид

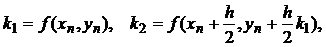
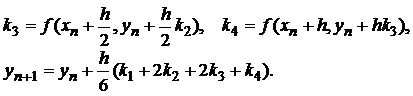
Эффективная оценка погрешности метода Рунге-Кутта затруднительна. Если число p определено, то для грубой оценки погрешности метода можно использовать так называемый принцип Рунге или метод двойного счета.

Пусть известно, что на каждом шаге допущена погрешность, приблизительно пропорциональная 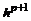(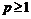), и 2 m представляет собой общее число шагов вычисления.

В таком случае, предполагая, что погрешность на каждом шаге одна и та же, приближенно получим

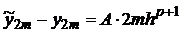, (4)

где 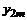- значение точного, а - приближенного решения в точке , A – неизвестный числовой множитель.

Согласно Рунге, производим тем же методом вторичный пересчет искомого решения y с двойным шагом H=2h. Тогда в силу нашего предположения будет допущена погрешность

(5)

где 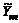- значение искомой функции в точке 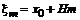, вычисленное с шагом H=2h.

Из формул (4) и (5) получаем

.

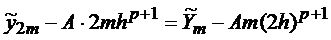Отсюда находим неизвестную постоянную

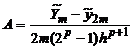
и, следовательно,

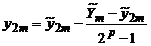
Таким образом, приближенно можно положить

,

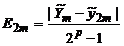где 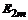- погрешность вычислений приближенного значения .

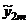Применив принцип Рунге для оценки погрешности классического метода Рунге-Кутта с p =4, получим

.

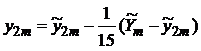Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчет (принцип Рунге). А именно, исходя из текущего верного значения y(x_i), вычисляют величину y(x_i+2h) двумя способами: один раз с шагом h, а второй раз с двойным шагом 2 h. Если расхождение полученных значений не превышает допустимой погрешности, то шаг h для данного этапа выбран правильно. В противном случае шаг уменьшают в два раза и повторяют указанную процедуру для нового шага.

Схемы Рунге-Кутта имеют ряд важных достоинств:

1) Все они имеют хорошую точность.

2) Они являются явными, т.е. значение y_{n +1} вычисляется по ранее найденным значениям за определенное число действий по определенным формулам.

3) Все схемы допускают расчет с переменным шагом; значит, нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае.

4) Для начала расчета достаточно выбрать сетку 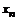и задать значение 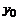; далее вычисления идут по одним и тем же формулам.

Лекция№11 МНОГОШАГОВЫЕ СХЕМЫ. МЕТОДЫ АДАМСА.

1. Мы рассмотрели методы Рунге-Кутта для численного решения задачи Коши для обыкновенного дифференциального уравнения первого порядка:

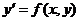(1)

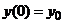(2)

Эти методы являются одношаговыми: при определении нового значения 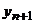используется лишь значение 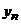. В общем случае для определения приближенного значения 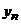искомого решения можно рассмотреть m-шаговые разностные схемы (m ≥1), т.е. уравнения вида:

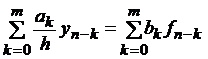, n = m, m +1, …, (3)

где a_k, b_k – числовые коэффициенты, f_n-k = f (x_n-k, y_n-k), a₀ ≠ 0, b_m ≠ 0.

В частности, при m =1, b₀ = 0, b₁ = a₀ = - a₁ = 1 получаем схему Эйлера.

Схема (3) называется явной (экстраполяционной), если b₀ =0 и значения 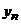определяются через предыдущие значения 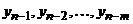по явной формуле

.

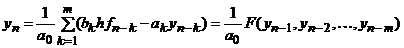Вычисления начинаются с n = m. Чтобы найти 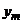, надо задать m начальных значений 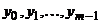, их можно найти, например, методом Рунге-Кутта, который использует лишь одно начальное значение .

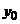Если b₀ ≠0, то схема (3) называется неявной (интерполяционной): для нахождения 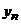при каждом n приходится решать нелинейное уравнение

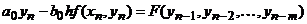(4)

Это нелинейное уравнение можно решать, например, методом Ньютона.

Погрешность аппроксимации схемы (3) на решении 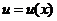уравнения (1), или невязка, определяется по формуле

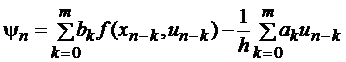(5)

Говорят, что схема (3) имеет s -й порядок аппроксимации (или просто, что схема (3) имеет s -й порядок), ес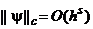ли

или , s >0. (6)

Коэффициенты a_k, b_k подбирают, исходя из соображений аппроксимации и устойчивости. Без нарушения общности можно считать, что

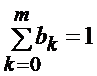(7)

т.к. коэффициенты уравнения (3) определяются с точностью до множителя. Разлагая ψ_n по степеням h и требуя, чтобы невязка имела заданный порядок, получаем условия для определения a_k, b_k. Так как u =1 есть решение уравнения (1) при f =0, из (3) следует, что

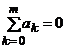(8)

Обычно для построения схем (3) применяют другие приемы, использующие интерполяционные и квадратурные формулы. Так, интегрируя дифференциальное уравнение (1) по x в пределах от 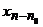до x_n, получаем

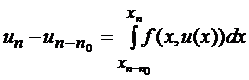(9)

Чтобы получить отсюда разностную схему, можно использовать для вычисления интеграла какую-либо квадратурную формулу.

2. Методы Адамса. Каждая квадратурная формула порождает соответствующий метод численного решения обыкновенного дифференциального уравнения (1). Заменим в тождестве

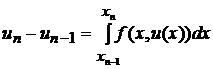, (10)

которое получается из тождества (9) при n ₀=1, интеграл квадратурной формулой

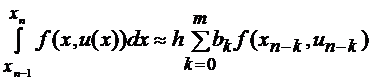(11)

Учитывая (10) и (11), можно записать разностную схему Адамса

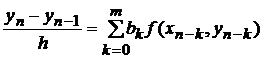(12)

Она может быть получена из (3), если положить a ₀=1, a ₁=-1, a ₂=…= a_m =0.

Квадратурная формула (11), на основе которой построена схема Адамса, содержит узлы сеток, не принадлежащие отрезку интегрирования 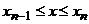. Обычно используется требование, чтобы квадратурная формула была точной для многочлена степени m. При этом выбирается интерполяционный многочлен с узлами .

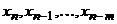При таком построении схемы погрешность ее аппроксимации совпадает с погрешностью квадратурной формулы. В самом деле, невязка для схемы (12)

.

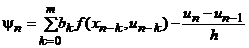Подставляя сюда выражение (10), получаем формулу для невязки

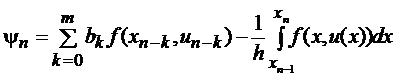(13)

3. Явные и неявные схемы. Если b ₀≠0, то схема (12) является явной и

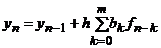(14)

Простейшим примером явной одношаговой схемы Адамса является схема Эйлера

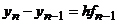при m =1, b ₀=0, b ₁=1.

Если положить в (12) m =1, b ₀=1, b ₁=0, то получим неявную одношаговую схему Адамса:

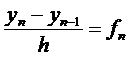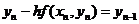или (15)

При m =1, b ₀= b ₁=1/2 получаем неявную симметричную одношаговую схему, имеющую второй порядок аппроксимации:

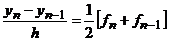(16)

Для определения значения y _n надо решать при каждом n нелинейное уравнение вида 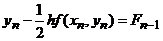, где .

Рассмотрим теперь двухшаговые схемы Адамса, соответствующие m =2.

Явная двухшаговая схема имеет вид

(17)

Здесь m=2, b₀=0, b₁=3/2, b₂=-1/2. Эта схема имеет второй порядок аппроксимации

.

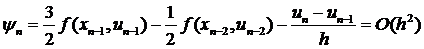Напишем двухшаговую неявную схему Адамса. Требуя, чтобы квадратурная формула (10) была точна для полиномов степени 0, 1, 2, находим коэффициенты b₀=5/12, b₁=8/12,
b₂=-1/12. Схема (11) имеет вид

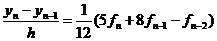(18)

4. Общие замечания. При выборе того или иного численного метода учитывается много обстоятельств, таких как объем вычислений, требуемый объем оперативной памяти ЭВМ, порядок точности, устойчивость по отношению к погрешностям округления и др. Мы рассматривали всюду методы с постоянным шагом h = x_{n +1}- x_n. Переход к переменному шагу h_n+1 = x_{n +1}- x_n носит формальный характер и для одношаговых схем не приводит к каким-либо новым принципиальным вопросам. Для многошаговых схем (m ≥2) формулы меняются.

В общем случае решение может быть сильно меняющейся немонотонной функцией. Естественно пользоваться неравномерной сеткой и уменьшать шаг (сгущать сетку) в области быстрого изменения функции u (x), чтобы обеспечить более точное приближение u (x) сеточным решением. Однако поведение решения заранее неизвестно. Поэтому на практике поступают так. Проводят сначала расчет на равномерной сетке; если видно, что на некотором интервале x_*<x<x^* решение сильно меняется, то на этом интервале сетка сгущается, и проводится новый расчет на неравномерной сетке. Вообще рекомендуется проводить расчеты на нескольких сгущающихся сетках. Если при сгущении сетки решение меняется мало, то нужная точность достигнута. В ходе расчета может оказаться необходимым использовать схемы разного порядка точности в разных областях изменения аргумента.

Методы Адамса являются менее трудоемкими по сравнению с методами Рунге-Кутта. Недостатком методов Адамса является начало вычислений: для определения 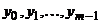обычно используется метод Рунге-Кутта. Для двухшаговых (и тем более многошаговых) схем Адамса изменение шага h требует усложнения формул, в отличие от метода Рунге-Кутта. На практике используется комбинация методов Рунге-Кутта и Адамса с программой автоматического выбора шага для получения заданной точности.

Л12 Общий метод определения параметров функциональной зависимости..

До сих пор мы рассматривали аппроксимирующие функции, линейно зависящие от параметров, и для этого частного случая давались эффективные методы определения параметров. Рассмотрим общий метод определения параметров функциональной зависимости, не предполагая ее линейности относительно параметров.

Пусть для совокупности упорядоченных значений (x_i, y_i), i =1,2,…, n построена функциональная зависимость 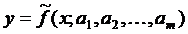, (1)

содержащая m параметров (m < n), причем функция 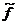имеет непрерывные частные производные по всем своим аргументам. Требуется определить 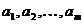так, чтобы формула (1) оказалась согласованной с исходными данными, т.е. невязки (уклонения)

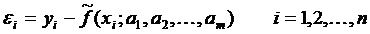
должны быть как можно меньше по абсолютной величине.

Если бы исходные данные не содержали ошибок и зависимость 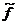была точной, то задача отыскания параметров a_i (i =1,2,…, m) свелась бы к решению m (m < n) уравнений из следующей системы n уравнений

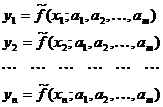(2)

Заметим, что система (2) является переопределенной.

Однако на практике, ввиду отсутствия указанных обстоятельств, система (2) обычно является несовместной, т.е. значения 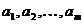, найденные из некоторых m уравнений, не удовлетворяют остальным n-m уравнениям.

Для приближенного решения системы (2) поступают следующим образом: каким–либо способом (например, графически или путем решения выбранных m уравнений системы (2)) находят грубые значения параметров .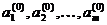

Пусть 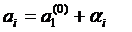(i =1,2,…,m) (3)

где α_i – поправки, считающиеся малыми, и 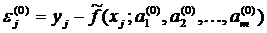- соответствующие невязки. Подставляя (3) в уравнения (2) и разлагая правые части полученных уравнений по степеням α_i , удерживая лишь члены первого порядка относительно α_i, будем иметь

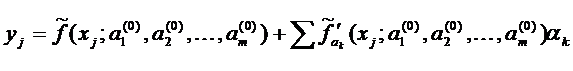(j =1,2,…, n) (4)

Для сокращения записи введем обозначения

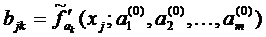(j =1,2,…, n; k=1,2,…,m)

Тогда равенства (4) перепишутся в виде

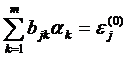(j =1,2,…, n) (5)

Система (5) линейна относительно неизвестных α_i и является, вообще говоря, несовместной, т.к. число уравнений в ней больше числа неизвестных.

Уравнения системы (5) называются условными, а сама система – системой условных уравнений. Система условных уравнений может быть решена в известном смысле, например, методом наименьших квадратов.

Подставляя в нелинейную систему (2) найденные значения 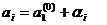(i =1,2,…, n) можно определить новые невязки ε_j⁽¹⁾ и в случае необходимости повторить процесс.

Л13 Среднеквадратичное приближение фун кций.

Интерполяция позволяет легко аппроксимировать функцию y(x). Однако точность такой аппроксимации гарантирована лишь в небольшом интервале порядка нескольких шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. На практике же всегда желательно иметь единую приближенную функцию , пригодную для большого отрезка . Поэтому далее будем сравнивать заданную и аппроксимирующую функции на большом отрезке. При интерполяции мы приравниваем значения y(x) и φ(x) в заданных точках x_i, называемых узлами сетки. Если y (x_i) определены неточно, например, получены в результате измерений в ходе проведения эксперимента, то точное приравнивание неразумно. Поэтому нередко целесообразней приближать функцию не по точкам, а в среднем, т.е. в норме линейного пространства.

Пусть заданы функция y(x) и множество функций φ(x), принадлежащие линейному нормированному пространству функций.

Можно поставить две задачи.

1. Аппроксимация с заданной точностью: по заданному ε найти такую φ(x), чтобы выполнялось неравенство .

2. Нахождение наилучшего приближения, т.е. функции , удовлетворяющей соотношению

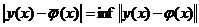. (1)

Существует ли наилучшее приближение и единственно ли оно (для данных функций и множества)? Оказывается, что ответ на этот вопрос утвердителен не при любом выборе пространства и множества. Но в любом линейном нормированном пространстве наилучшее приближение

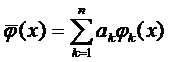(2)

где - система линейно независимых функций, существует, хотя не во всяком линейном пространстве оно единственно.

Рассмотрим гильбертово пространство 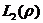действительных функций, интегрируемых с квадратом с весом ρ(x)>0 на заданном отрезке [ a,b ]. Норма в нем 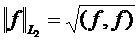, где скалярное произведение определяется следующим образом:

.

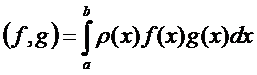Выберем в качестве аппроксимирующей функции линейную комбинацию (2). Подставляя ее в условие наилучшего приближения (1), получим

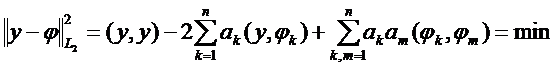
Приравнивая нулю производные по коэффициентам, получим систему линейных уравнений

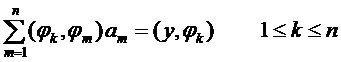(3)

Ее определитель есть определитель Грамма функций φ _k (x); поскольку функции линейно независимы, он отличен от нуля. Следовательно, наилучшее среднеквадратичное приближение существует и единственно. Для его нахождения необходимо решить систему линейных алгебраических уравнений (3).

Линейно-независимую систему функций можно ортогонализировать. Пусть φ _k (x) уже образуют ортонормированную систему, т.е. 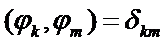; тогда формулы (3) резко упрощаются и становятся удобными для вычислений

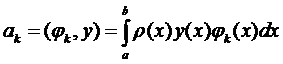
Это коэффициенты Фурье, так что наилучшее приближение есть отрезок обобщенного ряда Фурье.

Если функции φ _k (x) образуют полную ортонормированную систему, то в силу неравенства Парсеваля

Значит, при n →∞ норма погрешности бесконечно убывает, т.е. наилучшее приближение среднеквадратично сходится к y (x), и возможна аппроксимация с любой точностью.

Отметим, что если φ _k (x) не ортогональны, то при n →∞ определитель Грама обычно быстро стремится к нулю, система (3) становится плохо обусловленной, т.е. ее решение связано с большой потерей точности, и больше 5 - 6 членов брать нецелесообразно.

Для среднеквадратичной аппроксимации удобнее в качестве φ _k (x) брать многочлены, ортогональные с заданным весом. Наиболее употребительны среди них многочлены Якоби (частным случаем которых являются многочлены Лежандра и Чебышева), Лагерра и Эрмита. Для аппроксимации периодических функций используют тригонометрический ряд, он соответствует ρ(x)=1.

Все указанные системы функций полные, так что наилучшие приближения по ним сре-днеквадратично сходятся при n →∞, если y (x) интегрируема с квадратом с заданным весом.

Метод наименьших квадратов. Если вещественные функции определены таблично, т.е. на конечном множестве точек x ₁, x ₂,…, x_n, то их скалярное произведение можно определить формулой

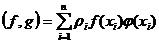, ρ_i >0, n – число узлов таблицы. Условие наилучшего приближения принимает вид

.

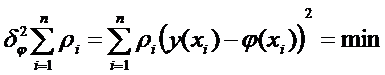Здесь φ – функция среднеквадратичного приближения.

Обозначим 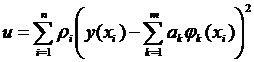, m ≤ n.

Используя необходимое условие экстремума функции, имеем

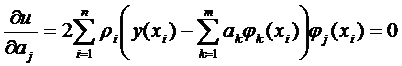
или

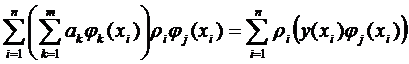, j =1,2,…, m.

Этот способ нахождения аппроксимирующей функции называется способом наименьших квадратов.

Метод наименьших квадратов широко используют для обработки экспериментальных кривых, точки которых получены в результате измерения с заметной погрешностью ε. В этом случае весу ρ _i придают смысл точности измерения в данной точке: чем выше точность, тем большее значение веса приписывают данному значению (например, ρ_i =ε^-2). Аппроксимирующая кривая будет проходить ближе к точкам с большим весом.

Если число коэффициентов аппроксимации m взять равным n, то среднеквадратичная аппроксимация совпадет с лагранжевой аппроксимацией. Очевидно, что при наличии значительных ошибок эксперимента интерполяция неразумна. Так как при m ≈ n среднеквадратичная аппроксимация близка к интерполяции, то хорошее сглаживание ошибок эксперимента будет при m < n, но если m слишком мало, то для описания сложной кривой коэффициентов может не хватить. Должно существовать какое-то оптимальное значение m, оно зависит от заданной функции y (x), числа узлов n, их расположения и выбранной системы φ_к(x).

Оптимальное число коэффициентов определяют следующим образом. Выбирают некоторое m, находят коэффициенты a_k, 1≤ k ≤ m, вычисляют полученное при этом среднеквадратичное уклонение по формуле

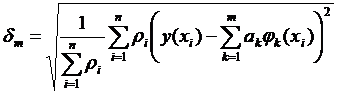
и сравнивают его с известной погрешностью эксперимента. Если δ_m>> ε, то число коэффициентов недостаточно для приближения y (x) и надо увеличить m. Если δ_m << ε, то старшие коэффициенты физически недостоверны и надо уменьшить m. Если δ _m ≈ ε, то m оптимально. Если при этом m << n, то вид аппроксимирующей функции выбран удачно. Если же m _опт≈ n, то следует поискать более подходящий вид аппроксимирующей функции.

Частные случаи.

1. Полиномиальная аппроксимация.

, k =0, 1, …, m.

Аппроксимирующий полином имеет вид: 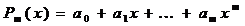, весовая функция ρ(x) принимается тождественно равной единице. Тогда имеем

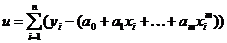
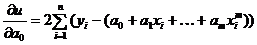
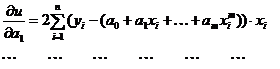
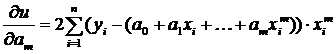
Система уравнений относительно искомых коэффициентов a_k, 0≤ k ≤ m записывается в виде:

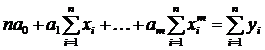
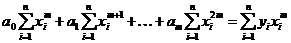
Определитель этой системы отличен от нуля, и полином наилучшего среднеквадратического приближения существует и единствен. Обычно m выбирают из диапазона от двух до пяти.

2. .

При этом 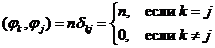, тогда .

Эти формулы можно использовать и при больших m.

Не нашли, что искали? Воспользуйтесь поиском: