Метод Эйлера решения задачи Коши. Алгоритм и оценка погрешности

Пусть дано дифференциальное уравнение

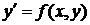. (1)

Допустим, что функция f (x, y) задана и непрерывна в некоторой области D вещественной плоскости. В области D требуется найти решение y (x) дифференциального уравнения (1), проходящее через заданную начальную точку

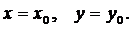(2)

При численном решении уравнения (1)-(2) задача ставится так: в точках 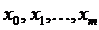нужно найти приближения 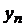для значений точного решения 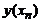. Разность 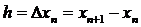называется шагом сетки. Во многих случаях можно считать, что h – постоянная, не зависящая от n. Полагаем, что h >0.

Многие приближенные методы опираются на уравнение

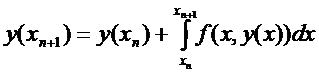, (3)

которое получается интегрированием уравнения (1) на отрезке 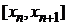; при этом интеграл в правой части (3) заменяется тем или иным приближенным выражением.

Метод Эйлера (другое название - метод ломаных) состоит в том, что при вычислении значения y_{n+ 1}по одному приближенному значению y_n, согласно уравнению (3), интеграл в правой части заменяется простейшим образом – через произведение начального значения подынтегральной функции на шаг h (по формуле левых прямоугольников):

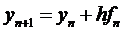, (4)

где .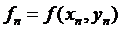

Геометрически схема (4) означает движение не по интегральной кривой, а по касательной к ней. На каждом шаге мы заново находим касательную, следовательно, траектория движения будет ломаной линией. Отсюда второе название метода Эйлера – метод ломаных.

Для оценки погрешности метода Эйлера предположим, что функция 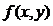в области D ограничена

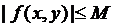, (5)

удовлетворяет условию Липшица по переменной y, т.е. существует такая постоянная K, что для любой пары точек с координатам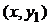и и 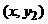, лежащих в области D, имеет место неравенство

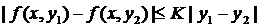. (6)

Предположим, кроме того, что функция 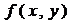в области D имеет ограниченную производную

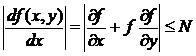. (7)

Назовем абсолютной погрешностью приближенного решения y_n величину

.

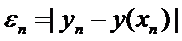Тогда можно показать, что для абсолютной погрешности 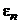имеет место следующая оценка

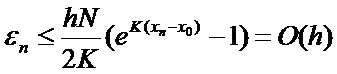. (8)

Таким образом, при h →0 и выполнении условий (5)-(7) приближенное решение сходится к точному равномерно (в области D) с первым порядком точности.

Метод Эйлера был описан Эйлером (1768) в его «Интегральном исчислении». Метод прост для понимания и программирования. Однако оценка (8) означает, что если желательно, скажем, получить 6 точных десятичных знаков, потребуется порядка миллиона шагов. Таким образом, этот метод является довольно грубым и применяется на практике только тогда, когда не требуется высокой точности и число шагов невелико.

Не нашли, что искали? Воспользуйтесь поиском: